AP Syllabus focus:
‘Recognize removable discontinuities and jump discontinuities in graphs and formulas, relating each type to how the function value and limit compare at the point.’
Understanding how functions can fail to be continuous is essential in calculus. Removable and jump discontinuities highlight different ways limits and function values can disagree at specific points.
Identifying Removable and Jump Discontinuities
Discontinuities occur where a function is not continuous at a point, meaning the limit and the function value do not align. In this subsubtopic, the focus is on distinguishing removable discontinuities and jump discontinuities by analyzing how limits behave relative to function values.
Understanding Discontinuities Through Limits and Function Values
A discontinuity arises whenever the behavior of a function near a point does not match the function’s value at that point. To classify the type of discontinuity, it is essential to evaluate both the left-hand limit, the right-hand limit, and the function value.
Discontinuity: A point where a function is not continuous because the limit does not exist, the function value does not exist, or the limit and function value do not coincide.
A function's behavior near a point provides critical information about how the graph should be interpreted in determining the discontinuity type.
Removable Discontinuities
A removable discontinuity occurs when the limit of a function exists at a point, but the actual function value is either missing or does not match the limit. Students often recognize this as a hole in the graph.
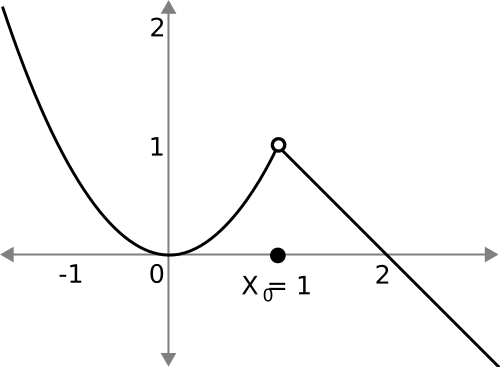
This graph shows a function with a removable discontinuity at x₀. The curve approaches the same y-value from both sides, but an open circle marks the point where the function is not defined or mismatched. This visually reinforces that the limit exists even though the function’s value at that point is not equal to the limit. Source.
Key Characteristics of Removable Discontinuities
A removable discontinuity typically satisfies the following conditions:
The left-hand limit and right-hand limit both exist and are equal at a point.
The function’s value at the point is either not defined or does not equal the common limit.
The limit describes predictable behavior, indicating that redefining the function value could “fix” the discontinuity.
Removable Discontinuity: A discontinuity where the two-sided limit exists but the function value is missing or inconsistent with that limit.
One important sentence serves here before introducing any further formal content, reinforcing that removable discontinuities represent a mismatch between predictable behavior and actual function definition.
How to Recognize Removable Discontinuities
Students should look for graphical or algebraic cues that indicate the presence of a hole rather than a break:
A plotted open circle at a point with no corresponding filled point.
A rational expression that becomes undefined because of a factor that can be canceled.
A two-sided limit that approaches a single value despite the function lacking the correct value at the discontinuity.
Jump Discontinuities
A jump discontinuity occurs when the left-hand and right-hand limits exist but are not equal. This results in a visible “jump” in the graph.
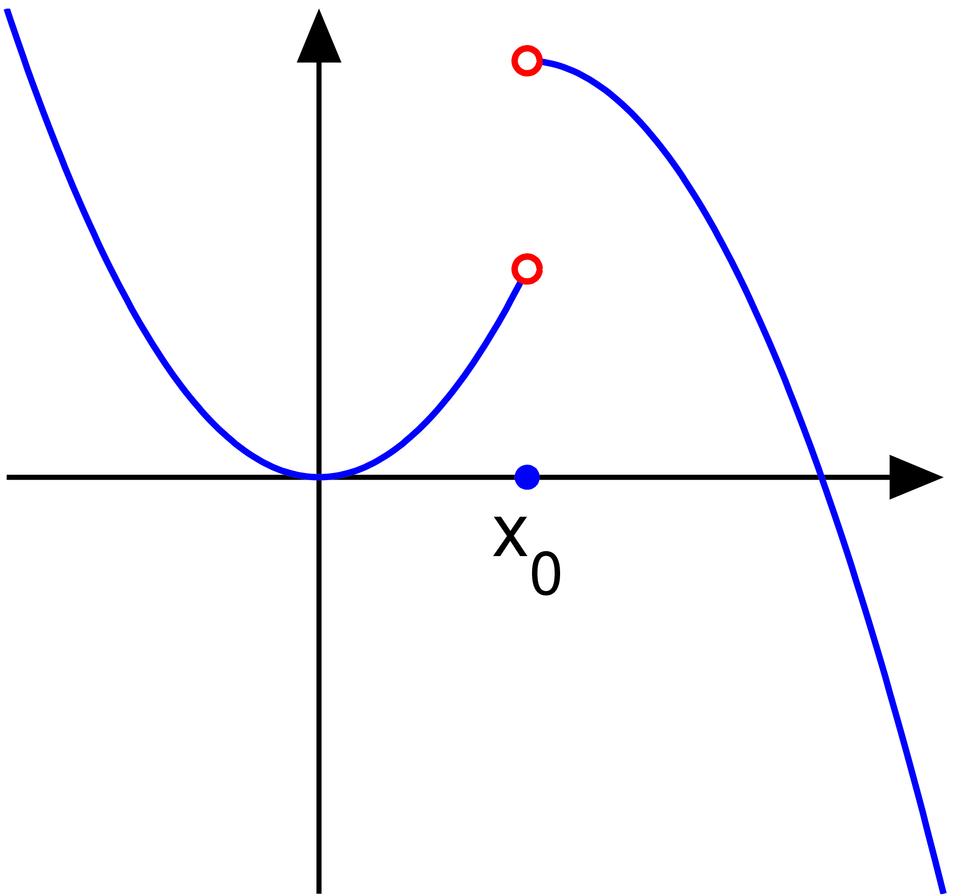
This diagram shows a function with a jump discontinuity at x₀. The left-hand and right-hand limits approach different finite values, producing a vertical jump in the graph. Because these one-sided limits disagree, no single limit exists at the point. Source.
Key Characteristics of Jump Discontinuities
Jump discontinuities display the following features:
The left-hand limit and right-hand limit approach different values.
The two-sided limit does not exist because disagreement between sides prevents a single value.
The function may assign either limit value, neither, or a completely different value at the point, but this does not affect the classification.
Jump Discontinuity: A discontinuity in which the left-hand and right-hand limits both exist but are unequal, causing the function to exhibit a jump at the point.
A sentence to bridge concepts: Jump discontinuities cannot be repaired by redefining the function, because no single value could reconcile the unequal one-sided limits.
Recognizing Jump Discontinuities in Graphs and Formulas
Jump discontinuities most often appear in:
Piecewise-defined functions, where expressions change abruptly at boundary points.
Graphs that show a sudden vertical shift from one connected segment to another.
Situations where each side of the function approaches a finite but different value.
Students should train themselves to observe how each side behaves independently near the discontinuity to determine whether the behavior constitutes a jump.
Comparing Removable and Jump Discontinuities
Clear differentiation between the two types supports deeper understanding of continuity and prepares students for advanced limit-based arguments.
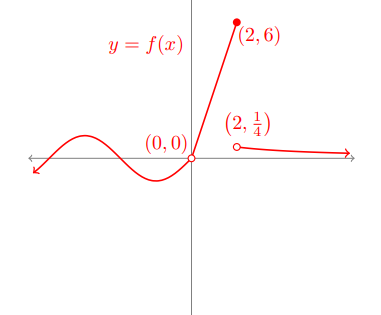
This graph illustrates both a removable discontinuity at the origin and a jump discontinuity at x = 2. The hole is shown with an open circle, while the jump is represented by two distinct one-sided values. The specific coordinates in the figure are incidental and simply serve to illustrate the two types of discontinuities together. Source.
Major Distinctions
Bullet-point comparison enhances clarity for learners:
Removable discontinuity:
The limit exists.
The function value is missing or incompatible.
Continuity could be restored by redefining the function.
Jump discontinuity:
Left and right limits exist but differ.
The two-sided limit does not exist.
No redefinition can eliminate the jump.
Why These Distinctions Matter
Removable discontinuities reinforce the importance of matching function values to limits, while jump discontinuities emphasize the difference between one-sided and two-sided behavior. Understanding both aids in interpreting function behavior and applying limit concepts accurately, especially when analyzing piecewise functions and preparing for derivative interpretations.
Students who master recognizing these discontinuity types gain stronger skills in limit evaluation, graphical interpretation, and continuity-based reasoning essential for success in AP Calculus AB.
FAQ
Focus on the behaviour of the curve itself rather than the plotted points.
If the curve visually approaches the same height from both sides, it is likely removable, even if the hole is not marked.
If the curve approaches two noticeably different heights, it indicates a jump.
When the graph is unclear, compare trends in the segments immediately to the left and right of the suspected point.
Yes. A function may be smooth on each side of the discontinuity but still jump at a specific point.
This typically happens in piecewise-defined functions where two smooth expressions meet at a boundary but do not connect.
The smoothness of each piece does not prevent a jump if their limit values differ.
Yes, especially when algebraic simplification hides the issue.
For example, cancelling a common factor may eliminate the expression that caused the discontinuity.
To avoid missing it, check the original form of the function before simplification:
• Identify values that make denominators or radicals undefined.
• Confirm whether the simplified form still reflects the domain restrictions.
Redefining a function at one point only adjusts its value at that point.
In a jump discontinuity, the left-hand and right-hand limits disagree. No single value could equal both, so the mismatch cannot be repaired.
Continuity restoration would require altering the function on at least one side, not merely assigning a point value.
Yes.
A removable discontinuity often suggests a missing or faulty measurement, such as a recording error or omitted data point.
A jump discontinuity typically signals an actual abrupt change in conditions, such as a sudden shift in temperature, voltage, or speed.
In applied contexts, identifying the type helps determine whether the discontinuity reflects real behaviour or merely a data artefact.
Practice Questions
Question 1 (1–3 marks)
The graph of a function f shows a single hole at x = 3. The left-hand limit and right-hand limit as x approaches 3 are both equal to 5, but f(3) is undefined.
a) State the type of discontinuity at x = 3.
b) Explain briefly why this discontinuity occurs.
Question 1 (1–3 marks)
a) Identifying a removable discontinuity: 1 mark
b) Explanation that the limit exists but the function value is missing or incorrect: 1–2 marks
Question 2 (4–6 marks)
A piecewise function g is defined as follows:
g(x) = 2x + 1 for x < 1
g(x) = 4 for x = 1
g(x) = x + 3 for x > 1
a) Determine the left-hand limit of g(x) as x approaches 1.
b) Determine the right-hand limit of g(x) as x approaches 1.
c) State whether g has a removable discontinuity, a jump discontinuity, or neither at x = 1.
d) Justify your conclusion using limit behaviour and the function value.
Question 2 (4–6 marks)
a) Correct left-hand limit calculation (2(1) + 1 = 3): 1 mark
b) Correct right-hand limit calculation (1 + 3 = 4): 1 mark
c) Correct identification of a jump discontinuity: 1 mark
d) Justification that the one-sided limits exist but are unequal, and therefore the two-sided limit does not exist: 1–2 marks

