Chain Rule with Inverse Trigonometric Composites (3.4.4) | AP Calculus AB Notes

AP Syllabus focus:
‘Apply the chain rule together with known inverse trig derivative formulas to differentiate expressions such as arcsin(2x), arctan(3x²), or arccos(f(x)).’

Composite expressions involving inverse trigonometric functions require careful application of the chain rule. Mastering the structure of inside and outside functions strengthens accuracy when differentiating inverse trig composites.

Understanding Composite Inverse Trigonometric Expressions

Composite inverse trigonometric expressions occur when an inverse trig function contains an inner function more complicated than a simple variable. Identifying this layered structure is essential because differentiation requires sequentially applying the chain rule, which ensures that both the outer inverse trig function and the inner function contribute correctly to the derivative.

When first encountering these expressions, students should recognize that arcsin, arccos, and arctan behave like other functions in composition: they operate on an input, and that input may itself be a differentiable function of x.

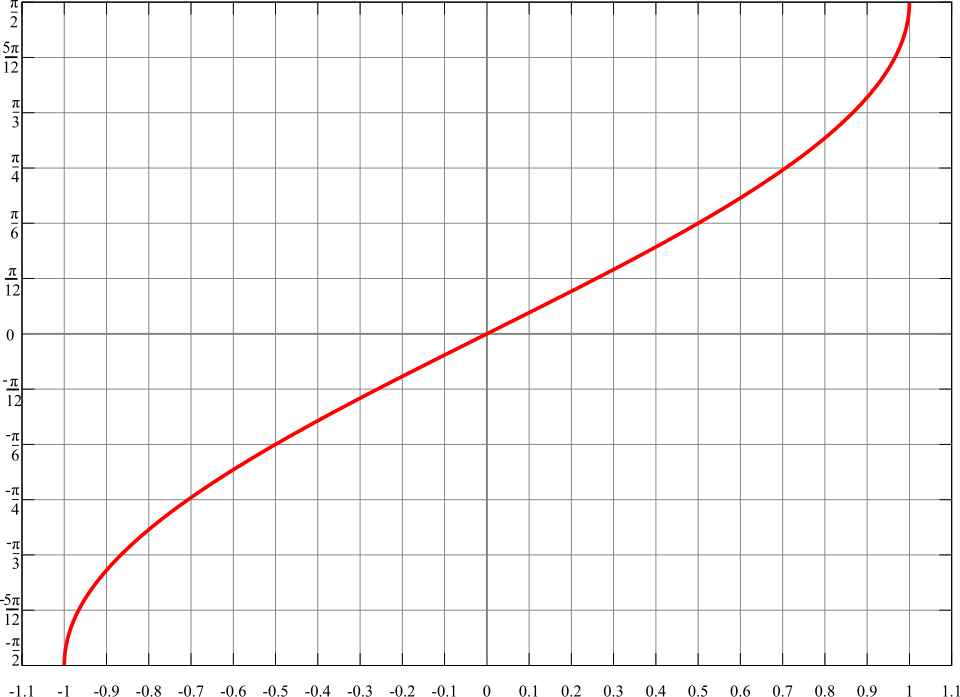
Graph of the inverse sine function y=arcsin⁡(x)y = \arcsin(x)y=arcsin(x) showing the domain [−1,1][-1,1][−1,1] and range [−π2,π2]\left[-\frac{\pi}{2}, \frac{\pi}{2}\right][−2π,2π]. This supports understanding composite expressions such as arcsin⁡(g(x))\arcsin(g(x))arcsin(g(x)). The graph reflects the principal branch that makes arcsin⁡\arcsinarcsin a proper function. Source.

Inverse Trigonometric Composite: An expression in which an inverse trigonometric function such as $\arcsin(x)$ , $\arccos(x)$ , or $\arctan(x)$ takes as its argument a differentiable inner function $u(x)$ .

Because inverse trig functions have established derivative formulas, combining them with the chain rule allows differentiation of expressions seen frequently in AP Calculus AB problems.

Derivative Forms for Inverse Trigonometric Functions

The derivative formulas for the three principal inverse trig functions play a central role. Each relates the rate of change of the inverse function to an algebraic expression involving its input.

$\frac{d}{dx}[\arcsin(u)] = \frac{1}{\sqrt{1-u^{2}}}\cdot \frac{du}{dx}$
$u$ = The differentiable inner function of $x$

Before applying additional formulas, it is important to understand how the chain rule embeds the derivative of the inner function within the expression.

A second derivative form is equally vital for composite expressions involving arccos, which mirrors the arcsin derivative but introduces a negative sign.

$\frac{d}{dx}[\arccos(u)] = -\frac{1}{\sqrt{1-u^{2}}}\cdot \frac{du}{dx}$
$u$ = The differentiable inner function of $x$

These relationships continue with the derivative of arctan, which produces a rational expression reflecting the geometry of the tangent and its inverse.

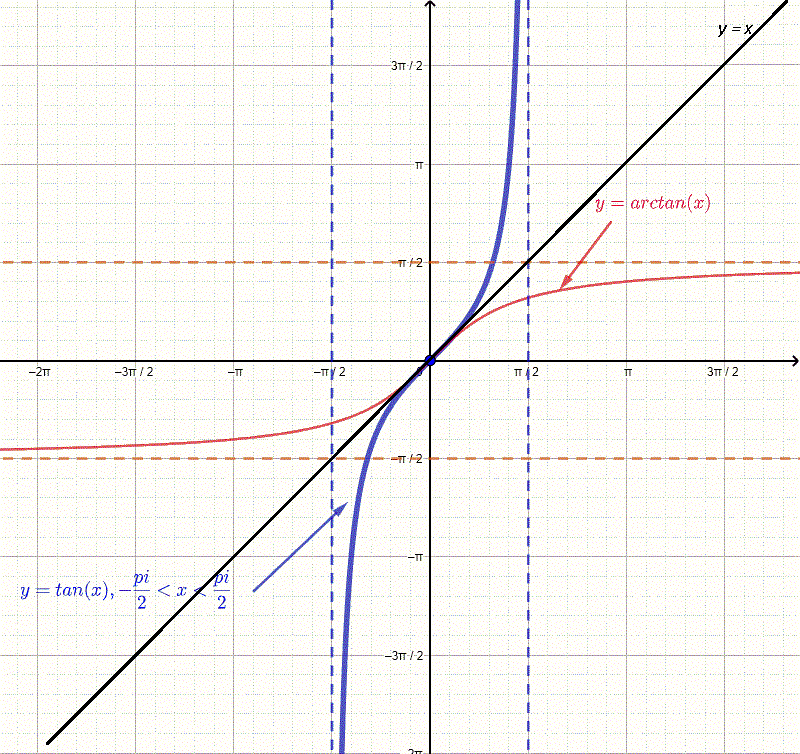
Graphs of y=tan⁡(x)y = \tan(x)y=tan(x) and its inverse y=arctan⁡(x)y = \arctan(x)y=arctan(x), reflected across the line y=xy = xy=x. This highlights how the inverse function’s range matches the restricted domain of tangent and visually reinforces the derivative relationship. Additional asymptotic details appear that extend beyond the immediate AP focus but enrich conceptual understanding. Source.

$\frac{d}{dx}[\arctan(u)] = \frac{1}{1+u^{2}}\cdot \frac{du}{dx}$
$u$ = The differentiable inner function of $x$

These formulas apply whenever the inverse trig function is differentiable and the inner function is itself differentiable with respect to x.

Applying the Chain Rule to Inverse Trig Composites

The chain rule states that when differentiating a composition of differentiable functions, the derivative equals the derivative of the outside function evaluated at the inside function multiplied by the derivative of the inside function. For inverse trigonometric composites, this means differentiating the inverse trig function first, keeping its inner expression intact, and then multiplying by the derivative of that inner expression.

General Strategy

To differentiate an expression of the form $\arcsin(g(x))$ , $\arccos(f(x))$ , or $\arctan(h(x))$ , use the following structured approach:

Identify the outer function.
The outer function will be an inverse trig function such as $\arcsin(\cdot)$ , $\arccos(\cdot)$ , or $\arctan(\cdot)$ .
Identify the inner function.
The inner function may be algebraic, trigonometric, exponential, or any differentiable expression in x.
Differentiate the outer function.
Apply the appropriate derivative formula for the inverse trig function, keeping the inside expression untouched.
Multiply by the derivative of the inner function.
This step completes the chain rule and ensures the composite structure is fully captured in the derivative.

Why the Chain Rule Is Essential

Inverse trigonometric derivatives inherently involve expressions containing the input variable inside radicals or rational forms. Without applying the chain rule, one would neglect how changes in the inner function affect the entire composite expression. This oversight would result in incomplete derivatives missing the critical term $\frac{du}{dx}$ .

Common Structural Variations

Students must be comfortable recognizing several common patterns:

Scalar multiples inside inverse trig functions, such as $\arcsin(2x)$ or $\arctan(3x^{2})$ , which require multiplying by the constant or polynomial derivative.
Functional compositions, such as $\arccos(f(x))$ , where $f(x)$ may itself require additional rules like the product or quotient rule.
Nested composites, occasionally requiring multiple sequential applications of the chain rule when the inner function is itself a composite.

Key Observations for AP-Level Mastery

Precise execution of the chain rule with inverse trig functions depends on understanding both structure and formula. Key ideas include:

Outer-then-inner differentiation preserves the composite nature.
Negative signs matter particularly for $\arccos$ , where an omitted sign produces significant algebraic errors.
Domains and restrictions of inverse trig functions influence interpretation but do not generally prevent symbolic differentiation in AP Calculus AB problems.
Clarity of notation helps organize layered derivatives, especially when inner functions require additional differentiation rules.

By consistently identifying the inner and outer components and applying the chain rule in a structured way, students develop fluency with differentiating inverse trigonometric composites across the full range of expressions required by the AP Calculus AB curriculum.

FAQ

Inverse trigonometric functions arise from restricting trigonometric curves to intervals where they are one-to-one. Their derivatives reflect these geometric constraints, producing expressions involving square roots or rational forms that control the allowable rate of change.

When a composite is formed, the inner function feeds directly into these expressions, preserving the structural form while adjusting the derivative through the chain rule.

Look for the inverse trig function symbol first; this nearly always marks the outer function in a composite. Everything inside its parentheses becomes the inner function, regardless of complexity.

For nested expressions, repeat this step layer by layer until all inside components are accounted for.

Students frequently forget to multiply by the derivative of the inner function, especially when the inner function is simple, such as a constant multiple.

Sign errors also appear often, particularly in derivatives involving arccos, where a missing negative sign changes the entire expression.

If the inner function contains products, quotients, or other composites, these must be differentiated correctly before being substituted into the inverse trig derivative.

For complex expressions, you may need:
• product rule
• quotient rule
• nested applications of the chain rule

Differentiation itself is unaffected by domain restrictions, but the resulting expression only makes sense where the inner function produces valid inputs for the inverse trig function.

This is especially important when interpreting solutions or assessing where the derivative is defined.

Practice Questions

Question 1 (1–3 marks)
Differentiate the function y = arccos(4x).
Give your answer in its simplest exact form.

Question 1 (3 marks total)
• 1 mark for identifying the need for the chain rule.
• 1 mark for correctly differentiating arccos(u) to obtain −1 / sqrt(1 − u²).
• 1 mark for multiplying by the derivative of the inner function 4x to obtain the final answer:
y' = −4 / sqrt(1 − 16x²).

Question 2 (4–6 marks)
Consider the function f(x) = arcsin(3x² − 1).
(a) Find f ’(x).
(b) The graph of y = f(x) is increasing on certain intervals. Using your answer to part (a), determine all x-values for which the graph is increasing.
Give exact values and justify your answer using the derivative.

Question 2 (6 marks total)

Part (a) (3 marks)
• 1 mark for applying the chain rule to arcsin(u).
• 1 mark for obtaining the derivative form 1 / sqrt(1 − (3x² − 1)²).
• 1 mark for multiplying by the derivative of the inner function 3x² − 1, giving:
f ’(x) = (6x) / sqrt(1 − (3x² − 1)²).

Part (b) (3 marks)
• 1 mark for using the condition f ’(x) > 0 to determine where the graph is increasing.
• 1 mark for noting that the denominator is always positive where the function is defined, so the sign depends on 6x.
• 1 mark for concluding that the graph is increasing when x > 0 (restricted further only by the domain of arcsin requiring −1 ≤ 3x² − 1 ≤ 1).

Try All Topic Practice Questions

Written by:

Dr Rahil Sachak-Patwa

Oxford University - PhD Mathematics

Rahil spent ten years working as private tutor, teaching students for GCSEs, A-Levels, and university admissions. During his PhD he published papers on modelling infectious disease epidemics and was a tutor to undergraduate and masters students for mathematics courses.