AP Syllabus focus:
‘Explain why a chosen rule or procedure is appropriate for a derivative problem, and compare different correct methods in terms of efficiency and clarity.’
Understanding how to justify a differentiation method strengthens conceptual reasoning, improves communication of mathematical thought, and ensures solutions reflect both accuracy and strategic choice rather than mechanical rule-application.
Choosing and Explaining a Differentiation Method
When differentiating an expression, AP Calculus AB students must do more than arrive at the correct derivative. They must also explain why a selected procedure is appropriate. This includes articulating which structural features of a function determine the differentiation rule and why alternative methods may be less efficient or less clear. The focus is on reasoning, not on performing lengthy calculations.
Recognizing Structural Features
A clear explanation begins with identifying the structure of the expression. The “structure” refers to how parts of the function relate to each other and which operations bind them. Students should describe these features explicitly so their reasoning is transparent.
Helpful structural markers include:
Products: Two variable expressions multiplied together.
Quotients: One expression divided by another.
Compositions: A function nested inside another.
Sums or Differences: Terms added or subtracted.
Constants or Coefficients: Multiplicative factors that simplify decisions.
Noting these characteristics guides the justification for rule selection and ensures the reasoning aligns with the form of the function rather than with memorized shortcuts.
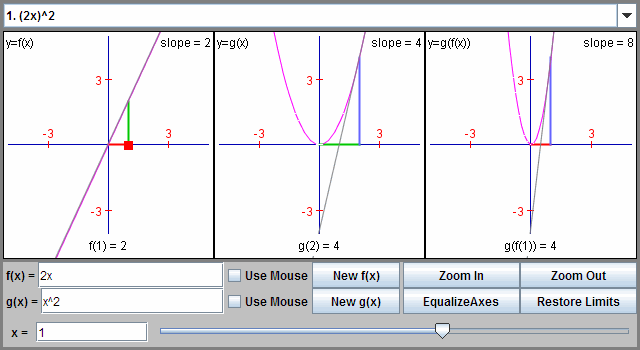
Three related graphs illustrate how an input moves through an inner and outer function, with tangent slopes showing that the derivative of a composite depends on both stages. The functions depicted are representative examples consistent with standard AP Calculus AB concepts. Source.
Justifying Rule Selection
Providing justification involves more than naming the rule. A strong explanation states why the rule applies and connects the rule directly to the structure of the function.
Product and Quotient Rule Justification
When explaining a choice involving multiplication or division, students should reference the presence of two differentiable expressions linked by multiplication or division.
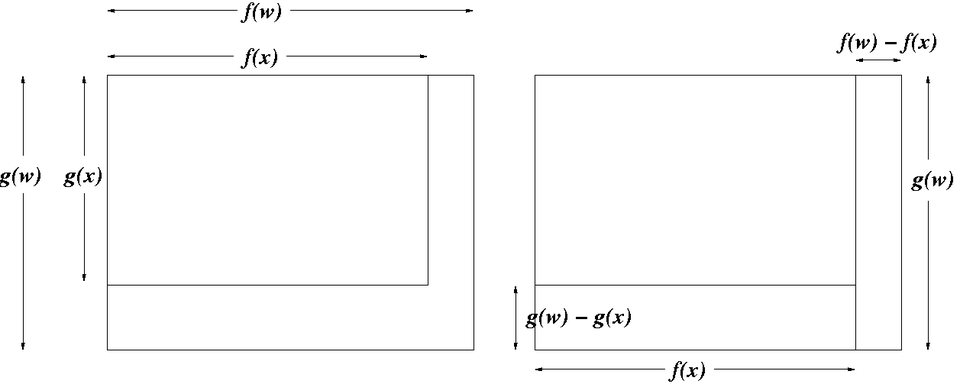
A labeled diagram presents the product rule in function notation, emphasizing that the derivative of a product requires combining and . The heading is in Catalan, but the mathematical notation matches AP Calculus AB conventions. Source.
They should emphasize that applying a simpler rule such as the power rule alone would ignore how each factor depends on the variable.
Chain Rule Justification
A justification involving the chain rule should highlight the presence of an inner function and an outer function. Students need to mention that because the input to one function is itself a function of the variable, differentiating correctly requires adjusting for the rate of change of the inner function. This connects their explanation directly to the layered structure of the expression.
Inner Function: The function inside another function in a composition, whose derivative must be accounted for when applying the chain rule.
A clear justification also contrasts the chain rule with an alternative method, noting that failing to apply the chain rule would treat the inner portion as constant, producing an incorrect derivative.
Efficiency and Clarity in Method Choice
The syllabus emphasizes comparing different correct methods in terms of efficiency and clarity. Students may encounter situations where more than one valid procedure exists. The expectation is to articulate why one method is preferable.
Identifying More Efficient Options
Efficiency arises when a rule simplifies work or reduces algebraic complexity. Students might justify efficiency by noting:
A substitution method rewrites the function into a cleaner form.
A rule reduces the number of differentiation steps.
A more direct method avoids unnecessary expansion or simplification.
Prioritizing Clarity
Clarity focuses on how understandable and traceable the method is. Students should prefer approaches that:
Reduce the chance of algebraic mistakes.
Follow a predictable sequence of steps.
Allow the logical structure of the derivative to remain visible.
Referring specifically to clarity demonstrates mathematical maturity and meets the requirement to explain methodological choices rather than simply implementing rules.
Comparing Multiple Correct Methods
When a problem allows more than one differentiation strategy, students should articulate why one is strategically stronger. A comparison should be explicit and grounded in mathematical reasoning rather than preference.
Key comparison points include:
Complexity of intermediate expressions.
Number of required rule applications.
Level of symbolic manipulation needed afterward.
How well the chosen method reflects the function’s structure.
A student might note that applying a product rule after expanding a polynomial is valid but less clear than applying the product rule directly, demonstrating thoughtful reflection on method choice.
Communicating Method Justification
Strong mathematical communication includes precise terminology, logical sequencing, and explicit reasoning. Students should aim to:
Use proper rule names (product rule, chain rule, etc.).
Reference specific parts of the function to support their decision.
State clearly why other approaches would be less effective, without dismissing their correctness.
Qualities of Effective Justification
Effective justifications typically:
Emphasize structural recognition.
Explain how the chosen rule directly matches that structure.
Address efficiency and clarity as part of the reasoning process.
Maintain focus on conceptual rationale instead of computational steps.
By explicitly grounding each decision in the underlying structure of a function and comparing methods thoughtfully, students demonstrate mastery of selecting and justifying differentiation procedures in alignment with the AP Calculus AB expectations.
FAQ
You should mention alternative methods when more than one rule could plausibly be applied and when comparing them clarifies why your chosen method is better.
This is especially useful when two approaches give the same final derivative but differ in efficiency, clarity, or the amount of algebra required.
Brief comparisons are sufficient; focus on explaining why your chosen method reflects the structure of the function more effectively.
Strong justifications often include explicit references to structure, such as “the expression is a composition,” “this term depends on x within another function,” or “these factors vary independently.”
Such language shows the examiner that you are reasoning about the form of the function, not simply naming a rule.
Avoid vague statements like “it looks easier” and instead point to identifiable mathematical features.
Even when the rule seems straightforward, you should still provide a brief explanation tied to the function’s structure.
A clear one-sentence justification is often sufficient, such as explaining that factors are multiplied or that one function is nested inside another.
The key is demonstrating awareness of why the rule fits, not providing lengthy exposition.
Yes, as long as the explanation is specific and accurate. Highlighting how an incorrect method could misrepresent the behaviour of part of the function can strengthen your justification.
You might reference:
Losing dependence on the inner function when ignoring the chain rule
Creating unnecessary algebraic complexity when expanding before differentiating
Compounding steps that increase the risk of mistakes
Such reasoning must remain concise and relevant to the given expression.
Practice scanning expressions for key structural markers such as compositions, products, or quotients before attempting any differentiation.
Develop a short mental checklist:
Are any functions nested?
Are expressions multiplied or divided?
Are terms simpler to differentiate if rewritten first?
With repetition, this recognition becomes automatic, making your justifications quicker and more confident in timed conditions.
Practice Questions
(1–3 marks)
A function is given by h(x) = (3x + 1) sin(x).
Explain why the product rule is the appropriate differentiation method for finding h'(x).
Question 1 (3 marks total)
• 1 mark: States that the function is a product of two differentiable expressions, (3x + 1) and sin(x).
• 1 mark: Clearly explains that the derivative must consider how both factors change and therefore requires the product rule.
• 1 mark: Rejects the use of the power rule or basic differentiation alone as insufficient, showing understanding of why those methods do not apply.
(4–6 marks)
A function is defined as f(x) = sqrt(g(x)), where g is a differentiable function.
(a) Explain why the chain rule is required to differentiate f.
(b) Suppose g(x) = x^3 − 2x. Justify the choice of method and then find f'(x).
(c) Comment on why expanding g(x) first would not provide a more efficient approach.
Question 2 (6 marks total)
(a) (2 marks)
• 1 mark: Identifies that f(x) = sqrt(g(x)) is a composition of an outer function (the square root) and an inner function g(x).
• 1 mark: Explains that because the input to the square root is itself a function of x, the chain rule must be used.
(b) (3 marks)
• 1 mark: Justifies using the chain rule by referencing the composition structure.
• 1 mark: Correctly substitutes g(x) = x^3 − 2x into f'(x).
• 1 mark: Produces a correct derivative, for example f'(x) = (1 / (2 sqrt(g(x)))) multiplied by g'(x), then g'(x) = 3x^2 − 2.
(c) (1 mark)
• 1 mark: States that expanding g(x) provides no simplification to the square root expression and would not reduce the number of differentiation steps, making it a less efficient method.

