Interpreting related rate answers requires translating symbolic results into meaningful statements about changing quantities, ensuring units, direction, and contextual significance are clearly communicated for accurate understanding of instantaneous change.

Interpreting and Explaining Related Rate Answers

Effectively explaining a related rate answer is a critical skill in applied differentiation. After computing a derivative-based rate, a student must articulate what quantity is changing, how fast it is changing, in what units, and at what specific moment the change occurs. These explanations turn symbolic differentiation work into meaningful descriptions of real-world behavior, aligning with the AP Calculus AB emphasis on contextual interpretation.

Identifying the Changing Quantity

When interpreting a related rate answer, the first priority is stating the specific dependent variable whose rate has been computed. This quantity should be named clearly using the language of the context. Students must ensure that when referencing a rate such as $\frac{dx}{dt}$, they indicate both variables: what is changing ($x$) and with respect to what it is changing ($t$). This reinforces the conceptual understanding that a related rate measures instantaneous change driven by variations in another quantity.

Interpreting the Meaning of a Rate

A related rate value represents an instantaneous rate of change, describing how one variable responds at the exact moment specified in the problem. Interpreting an answer requires converting the symbolic expression into a verbal explanation that connects to the physical, geometric, or contextual scenario. Students should avoid vague statements and instead articulate meaning explicitly through structured phrasing that includes direction and magnitude.

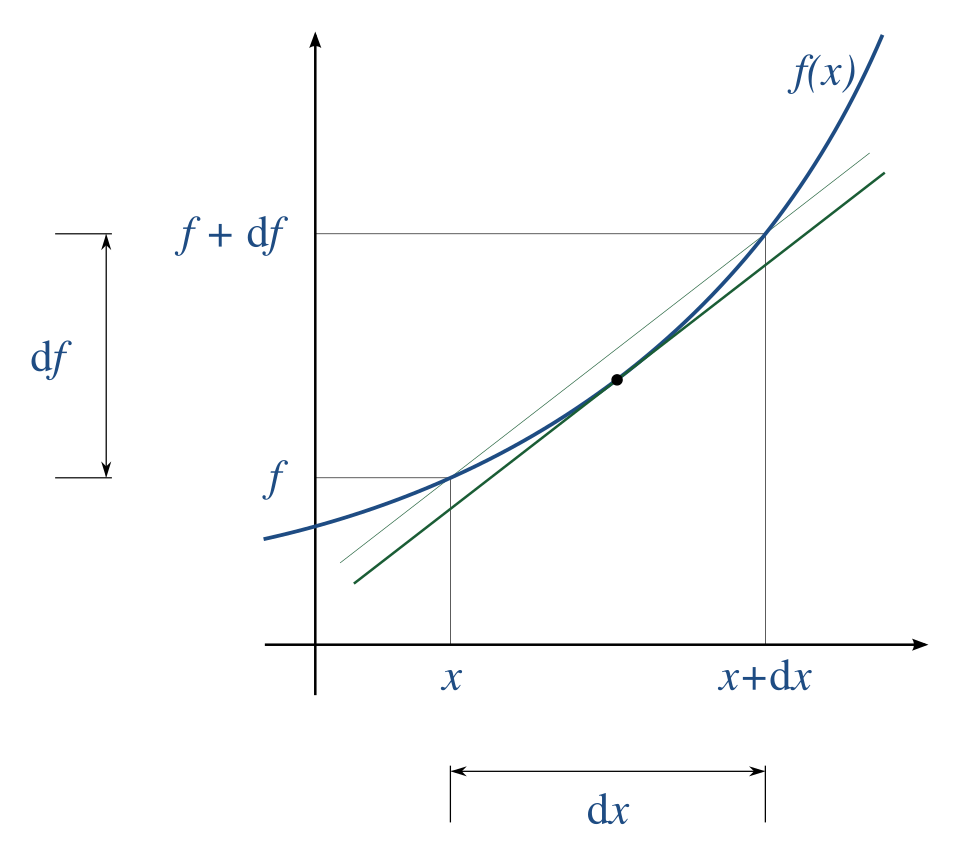
This diagram shows a curve $f(x)$ with a tangent line at a point, emphasizing that the derivative represents the instantaneous slope at that location. The labeled increments $dx$ and $df$ illustrate how a small input change corresponds to a small output change. Extra differential notation extends slightly beyond AP requirements but strengthens clarity regarding directional change. Source.

When applying this definition, students ensure their written interpretations reflect the moment-specific nature of related rates.

Emphasizing Units and Direction

A complete interpretation always identifies the units of the computed rate. Since related rates arise from differentiating relationships between physical or geometric quantities, the resulting units combine those of the variables involved and often produce compound expressions such as meters per second, square centimeters per minute, or radians per hour. Direction is expressed through the sign of the rate:

• A positive value indicates that the quantity is increasing at that instant.

• A negative value indicates that the quantity is decreasing at that instant.

These interpretations must be stated verbally. Magnitude alone never conveys complete meaning without direction and context.

Stating the Instant of Measurement

Related rate answers are always tied to a particular instant defined in the problem. Because derivatives represent instantaneous change, students must identify the moment at which the computed rate applies. This ensures the description does not suggest the rate applies generally but only under the specified conditions or geometric configuration.

Structuring a Complete Verbal Explanation

A polished related rate interpretation includes several essential elements, each conveyed clearly:

• Identify the quantity changing, using precise variable names or contextual descriptions.

• State the numerical rate, including sign and magnitude.

• Supply units, ensuring they accurately reflect the derivative’s structure.

• Clarify whether the quantity is increasing or decreasing based on the sign.

• Specify the instant at which the rate applies.

• Tie the statement back to the physical or geometric situation, showing that the rate makes sense in the stated context.

Each part ensures that the explanation reflects conceptual understanding rather than procedural computation alone.

Avoiding Common Interpretation Errors

Students frequently misinterpret related rate answers by omitting key contextual details. The most common issues include:

• Missing units, which leaves the rate dimensionally ambiguous.

• Ignoring the sign, resulting in unclear direction of change.

• Describing the rate as applying “always”, rather than at the stated instant.

• Restating the symbolic derivative without interpretation, which fails to demonstrate conceptual understanding.

Clear explanations prevent these errors and align results with AP expectations.

Communicating Contextual Meaning

Interpretation must always connect back to the real-world or geometric meaning of the variables. A correct explanation does more than state numerical results; it clarifies the practical significance of the computed rate. When a rate describes a shrinking radius, an expanding volume, or a moving object, the explanation should integrate that information naturally.

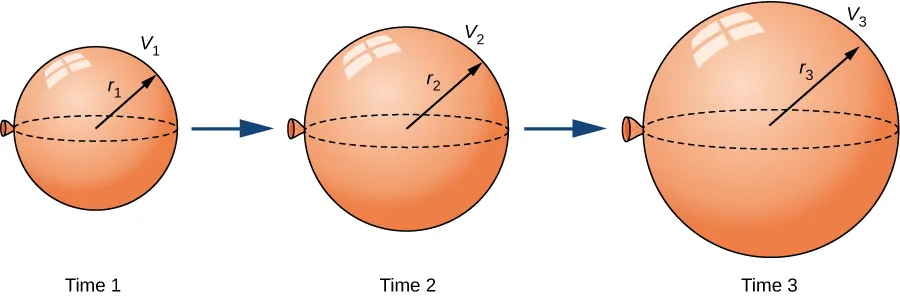
This figure shows a balloon at successive times with increasing radius ($r_1, r_2, r_3$) and volume ($V_1, V_2, V_3$). It emphasizes how related rates connect simultaneous changes in geometric quantities. The diagram reinforces the need to articulate which quantity is changing and in what direction at a specific moment. Source.

Refining Language for Precision

Precise academic language enhances clarity. Students should practice using consistent terminology such as “increasing,” “decreasing,” “at that instant,” and “with respect to time.” These expressions ensure no ambiguity when describing how and when a quantity changes. Verbal precision reflects mathematical precision and supports deeper conceptual understanding.

Final Checks for Interpretation Quality

Before writing a final interpretation, students can assess quality by confirming:

• The explanation answers what, how fast, in what direction, and when.

• The statement uses units correctly and consistently.

• The meaning aligns with the broader physical or geometric situation.

• The phrasing demonstrates clear comprehension of instantaneous change.