Second derivatives of implicit relations reveal how curves bend and change shape, extending concavity analysis to equations where y is not isolated as a function of x.

Understanding Second Derivatives in Implicit Contexts

When working with an implicit relation, we study an equation involving both x and y without rewriting it in explicit form. The second derivative gives insight into concavity and the curvature of the curve, even when expressing y directly as a function of x is difficult or impossible.

Geometrically, an implicit relation defines a curve in the plane even when the graph fails the vertical line test or cannot be written as a single explicit function y=f(x)y=f(x)y=f(x).

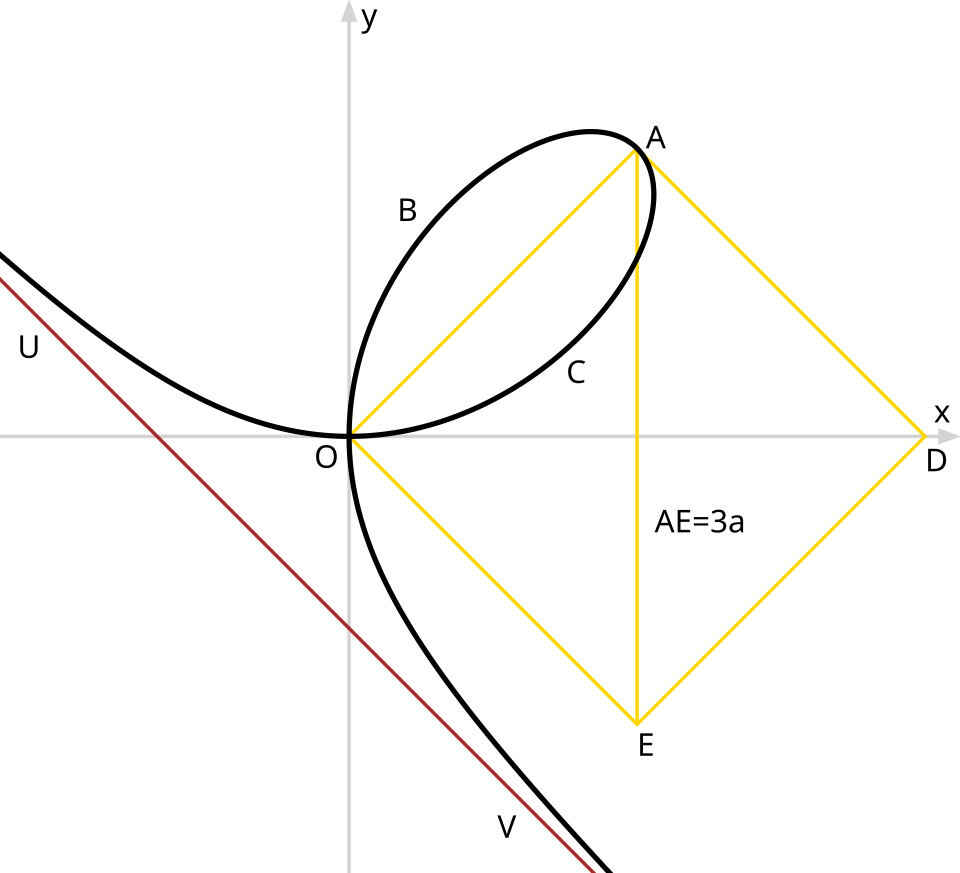
Folium of Descartes: an implicit curve defined by a single equation in $x$ and $y$. The loop and extending branch illustrate that implicit relations can produce shapes that are not functions of $x$. The specific equation extends slightly beyond the AP syllabus, but the image effectively visualizes curves analyzed using implicit first and second derivatives. Source.

Before second derivatives can be found, the first derivative must be obtained through implicit differentiation, which applies the derivative rules to both sides of the equation while treating y as a differentiable function of x. Only after this step can the second derivative be constructed.

Differentiating dy/dx Again with Respect to x

Once $\frac{dy}{dx}$ is known, the next step is to compute $\frac{d^2y}{dx^2}$. Because most implicit derivatives include a mix of both x and y, the process requires careful attention to several ideas:

Key Principles When Differentiating dy/dx Again

• Every appearance of y must be differentiated using the chain rule because y depends on x.

• Expressions containing $\frac{dy}{dx}$ must be differentiated using product or quotient rules when appropriate.

• The second derivative often involves all three quantities: x, y, and $\frac{dy}{dx}$.

• The final expression does not need to eliminate y unless a specific task requires it; the result is typically left implicit.

Because implicit relations frequently involve algebraic combinations of variables and derivatives, second derivatives tend to appear in more complex forms than their explicit-function counterparts.

Structure of a Second Derivative Expression

The second derivative is generally built by differentiating a rational or composite expression for $\frac{dy}{dx}$. This requires applying differentiation rules systematically and substituting back wherever necessary.

A sentence following the equation helps clarify that differentiation rules from earlier topics apply fully here, but with the added complexity that both variables and derivatives must be handled simultaneously.

Processes for Finding Second Derivatives

The procedure for determining a second derivative for an implicit relation can be organized into a structured sequence that supports accuracy:

Step-by-Step Process

• Differentiate the original equation implicitly to obtain $\frac{dy}{dx}$.

• Rewrite $\frac{dy}{dx}$ clearly, often as a single rational expression, to prepare for a second differentiation.

• Differentiate $\frac{dy}{dx}$ with respect to x, applying:

  • the product rule when factors involve both x and y

  • the chain rule when differentiating any term containing y

  • the quotient rule if $\frac{dy}{dx}$ is expressed as a quotient

• Replace each occurrence of $\frac{dy}{dx}$ that appears during the second differentiation with the original first derivative expression.

• Simplify carefully, allowing the second derivative to remain in implicit form.

These steps ensure that no derivative of y is overlooked and no implicit dependence is ignored.

Interpreting Second Derivatives from Implicit Relations

Because implicit second derivatives incorporate x, y, and $\frac{dy}{dx}$, interpreting them requires translating the expression into information about concavity or rate of change of slope.

Once d2y/dx2d^2y/dx^2d2y/dx2 has been computed for an implicit relation, its sign tells us whether the graph is bending upward (concave up) or bending downward (concave down) with respect to the x-axis.

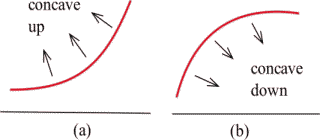
This graph illustrates a function that is concave up on some intervals and concave down on others. It demonstrates how a positive second derivative corresponds to upward curvature and a negative second derivative to downward curvature. The source discusses applications beyond the AP syllabus, but the visual depiction of concavity aligns directly with the study-note content. Source.

Using the Second Derivative to Describe Concavity

• A positive second derivative indicates the curve is concave up, meaning its slope is increasing.

• A negative second derivative indicates the curve is concave down, meaning its slope is decreasing.

• If the second derivative changes sign across a point where it is defined, the curve experiences a change in concavity.

These interpretations follow the same principles used for explicit functions, even though the algebraic form is more involved.

Common Structures and Features of Implicit Second Derivatives

Second derivatives for implicit relations often arise in expressions with the following characteristics:

Frequent Characteristics

• The presence of mixed variables, such as x terms multiplied by y terms.

• Dependence on dy/dx, which appears as a component rather than a final standalone value.

• Fractional forms created by quotient-rule applications.

• Multi-layered expressions requiring substitution and simplification.

Because implicit curves may loop, turn, or fold over themselves, the second derivative provides valuable geometric insight that is not always visible from the original relation alone.

Importance of Mastery for Analysis

Understanding how to find and interpret second derivatives for implicit relations equips students to analyze curvature and concavity in a far broader class of curves than those defined explicitly. The process reinforces derivative concepts from earlier topics while extending them into richer mathematical settings involving interdependent variables.