AP Syllabus focus:
‘The largest function value among the candidates is the absolute maximum, and the smallest function value among the candidates is the absolute minimum on the interval.’
Absolute extrema describe the highest and lowest values a function attains on a specified interval. Understanding how to compare candidate points ensures accurate identification of maximum and minimum values.
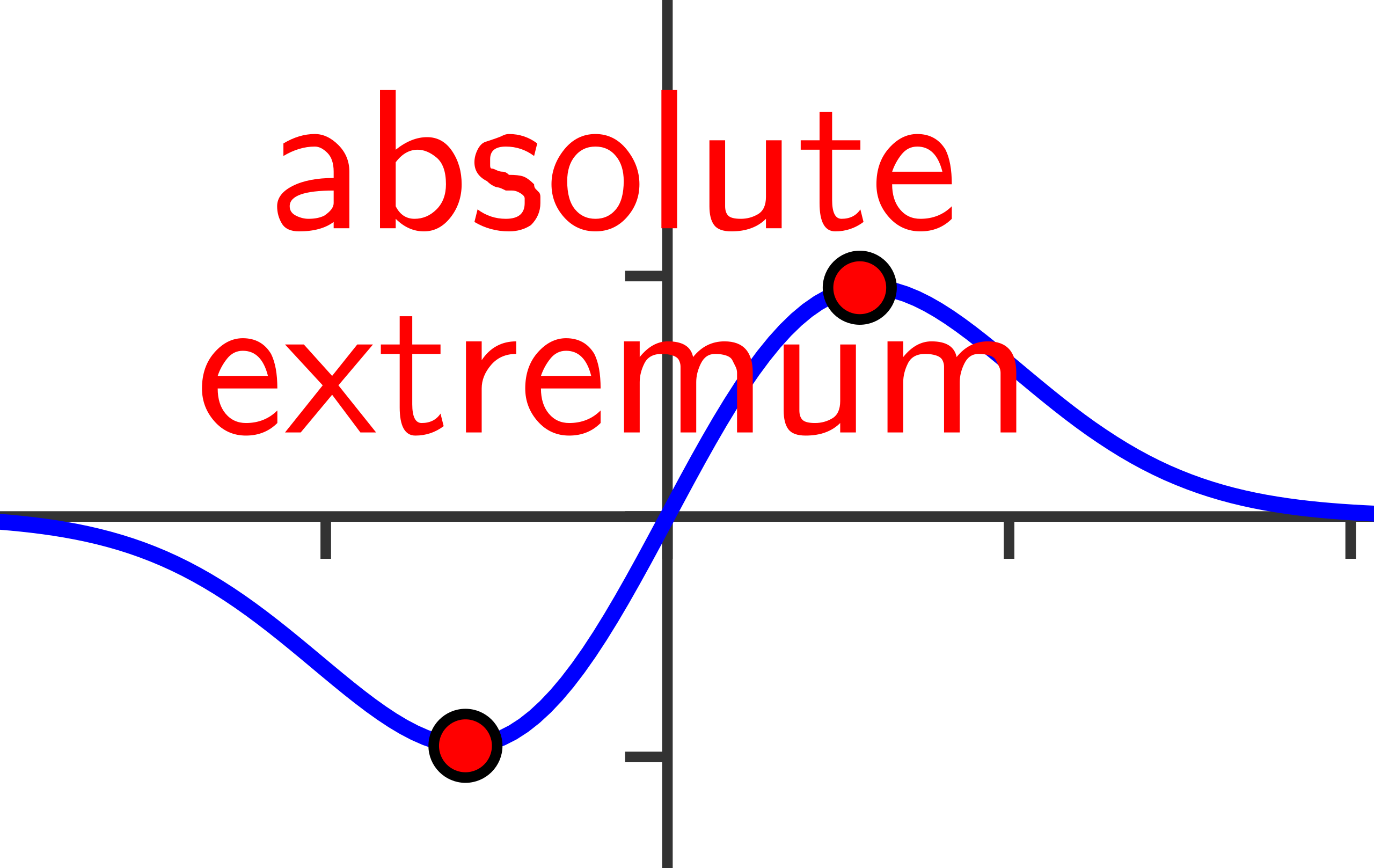
A graph of a continuous function on a closed interval with its absolute maximum and absolute minimum labeled. The diagram emphasizes the highest and lowest -values attained on the interval. This supports the idea that these extrema are identified by comparing function values at candidate points. Source.
Identifying Absolute Maximum and Minimum Values
The process of determining absolute extrema relies on evaluating a function at specific candidate points, which include critical points (where the derivative is zero or undefined) within the interval and the endpoints of the interval itself. Because the function is already assumed to be continuous on a closed interval for this subsubtopic’s focus, these values can be directly compared to find the largest and smallest outputs.
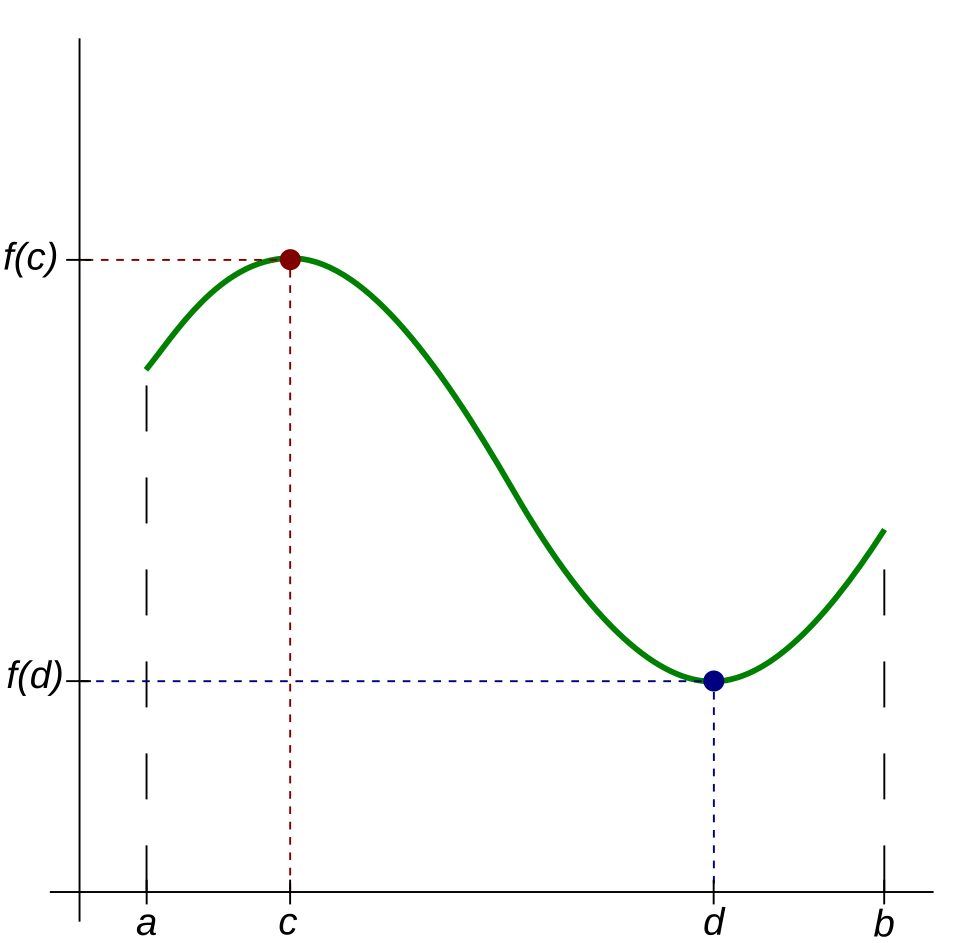
A graph of a continuous function on showing that it achieves both a highest and a lowest value on the interval. The marked points illustrate how continuity ensures the existence of absolute extrema. This supports the comparison of candidate points by confirming that extrema must occur somewhere on the interval. Source.
Meaning of Absolute Extrema
Absolute extrema represent the definitive highest and lowest values of a function on a given closed interval. Unlike local extrema—which only describe relative highs or lows compared with nearby points—absolute extrema require evaluating the function’s behavior across the entire interval.
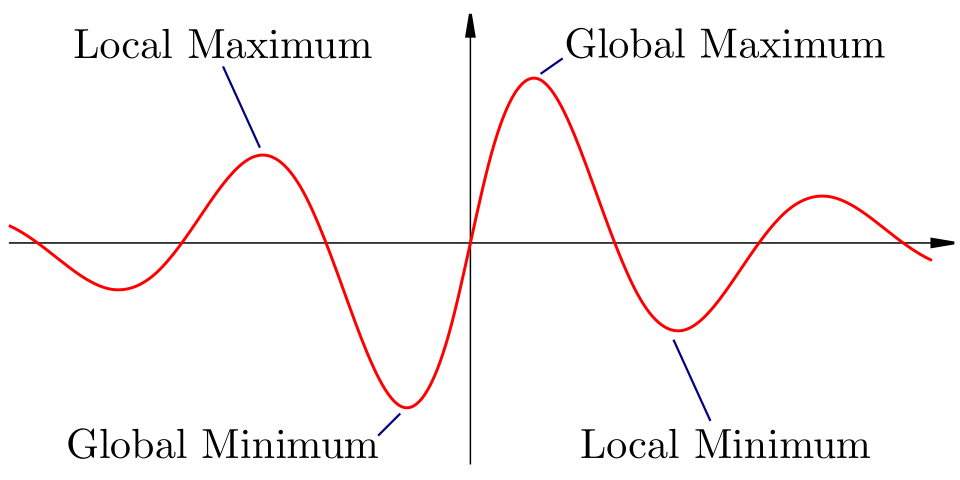
A graph showing several local maxima and minima along with global extrema of a damped oscillating function. The visual distinguishes between relative peaks/troughs and the absolute highest and lowest points. The extra oscillations extend beyond AP expectations but simply offer additional examples of extrema. Source.
The AP specification states that “the largest function value among the candidates is the absolute maximum, and the smallest function value among the candidates is the absolute minimum on the interval.” This emphasizes that identifying absolute extrema is a comparison task grounded in the output values of designated candidate points.
Understanding Candidate Points
When using the Candidates Test, students examine values at specific locations to determine whether they correspond to absolute maxima or minima. A candidate point is any point whose function value must be evaluated to determine if it is the absolute highest or lowest on the interval.
Candidate Point: A point in a closed interval that must be evaluated when searching for absolute extrema; includes critical points inside the interval and both endpoints.
Because the interval is closed, the function is guaranteed to have at least one absolute maximum and minimum, making each candidate point’s function value essential.
A candidate point arises in one of two ways:
It is a critical point, defined as a point where or where the derivative is undefined, provided is in the domain of .
It is an endpoint of the interval, which must always be included in absolute extrema determination.
The identification of candidate points ties together derivative behavior and interval structure, forming the foundation for evaluating extrema.
Evaluating Function Values at Candidate Points
Once all candidate points are identified, students determine absolute extrema by comparing their corresponding function outputs. This process is strictly numerical or evaluative rather than conceptual because identifying which value is largest or smallest is inherently a comparison task.
To reinforce the comparison procedure, consider the role of function output values:
The largest value among the candidate evaluations corresponds to the absolute maximum on the interval.
The smallest value among these evaluations corresponds to the absolute minimum on the interval.
This direct comparison approach highlights that even if a critical point represents a local extremum, it may or may not represent an absolute extremum, depending solely on the relative magnitudes of the function values at all candidates.
Structure of the Absolute Extrema Identification Process
Although this subsubtopic focuses on interpreting the results rather than performing the entire Candidates Test, recognizing the structure clarifies why evaluation is necessary. The identification process follows a list-based, comparison-driven approach.
Students should be able to clearly articulate:
Why certain points qualify as candidates.
How evaluating at each candidate contributes to determining extrema.
That absolute extrema depend on comparing outputs, not derivative signs alone.
Practical Interpretation of the Specification
The AP specification emphasizes that absolute extrema arise from comparing values, not from examining derivative behavior directly. The derivative is used only to locate critical points; the extrema themselves are determined solely by evaluating function values.
This distinction underscores the importance of the Candidates Test as a comparison tool: all candidate points are examined equally, and each function value is treated as a potential extremum until proven otherwise through comparison.
Essential Features of Absolute Maxima and Minima
The following bulleted list reinforces the characteristics of absolute extrema and their identification:
Absolute maximum: The greatest function value on the interval.
Absolute minimum: The smallest function value on the interval.
Critical points inside the interval are always candidates for extrema.
Endpoints are equally important candidates and must always be included.
The function must be continuous on a closed interval for guaranteed extrema.
All candidates must be evaluated even if some appear unimportant from the graph or derivative behavior.
Relationship to Function Behavior
Understanding absolute extrema provides insight into overall function behavior across an interval. Identifying the highest and lowest outputs gives a complete picture of how the function behaves on that domain, distinguishing overall trends from merely local changes.
This reinforces why comparing candidate values is central: only by examining each candidate’s function value can students make definitive claims about absolute maxima and minima.
FAQ
Absolute extrema concern the highest and lowest function values on a closed interval, not the steepness of the graph.
Slope information (from the derivative) helps locate critical points but does not indicate which point has the greatest or smallest function value.
Absolute extrema always depend on evaluating and comparing actual function outputs at candidate points.
A discontinuity at a candidate point can prevent a true absolute extremum from occurring there because the function may ‘jump’ around the point.
In such cases, an absolute extremum might still exist elsewhere on the interval, but the discontinuity means the value at the break cannot be treated with the same reliability as a continuous point.
Checking endpoints becomes especially important if continuity fails inside the interval.
A function can share the same absolute maximum or minimum value at multiple points if it reaches that same highest or lowest value more than once.
For example, a function could level off along a flat top or bottom segment.
In such cases, each point where the function equals that extremal value is an absolute maximum or minimum location.
Graphs can be deceiving, especially when drawn without precise scales or when endpoints lie far from prominent interior features.
Endpoints can produce values larger or smaller than critical points, even if the visual impression suggests otherwise.
Because the Candidates Test requires comparing all candidate outputs, excluding endpoints risks missing the true extremum.
The comparison requires enough precision to determine which output is largest or smallest.
If values are close, more accurate evaluation is needed to avoid misidentifying the extremum.
For exact algebraic expressions, no rounding is necessary.
For numerical values, ensure that any approximations still preserve the correct ordering of the function values.
Practice Questions
A function g is continuous on the closed interval [-2, 3]. The function has a single critical point at x = 1, where g(1) = 4. The endpoint values are g(-2) = -1 and g(3) = 5.
Using the information above, determine the absolute maximum and absolute minimum values of g on the interval.
(Total 3 marks)
• 1 mark: Identifying the candidate points as x = -2, x = 1, and x = 3.
• 1 mark: Correctly identifying the absolute maximum value as 5 at x = 3.
• 1 mark: Correctly identifying the absolute minimum value as -1 at x = -2.
A continuous function f is defined on the closed interval [0, 6]. The derivative f' has two critical points inside the interval at x = 2 and x = 4. Values of the function at the candidate points are:
f(0) = 7, f(2) = 3, f(4) = 12, and f(6) = 10.
(a) State the candidate points that must be evaluated to find the absolute extrema.
(b) Determine the absolute maximum and absolute minimum values of f on [0, 6].
(c) Explain why checking only the critical points would not be sufficient in this problem.
(Total 6 marks)
(a) (2 marks)
• 1 mark: Listing the endpoints x = 0 and x = 6.
• 1 mark: Listing the interior critical points x = 2 and x = 4.
(b) (3 marks)
• 1 mark: Correct absolute maximum value of 12 at x = 4.
• 1 mark: Correct absolute minimum value of 3 at x = 2.
• 1 mark: Statement that these values come from comparing all candidate outputs.
(c) (1 mark)
• 1 mark: Explanation that absolute extrema on a closed interval may occur at endpoints, so excluding endpoints could miss the true maximum or minimum.

