AP Syllabus focus:
‘Use the product rule (f·g)′ = f′g + fg′ to differentiate products of polynomial and power functions, simplifying results algebraically.’
The product rule is a fundamental differentiation tool that allows students to compute derivatives of expressions formed by multiplying two algebraic functions, ensuring accurate and efficient symbolic manipulation.
Understanding the Need for the Product Rule
When two functions are multiplied, the rate at which their product changes depends on how each function changes with respect to the input variable.
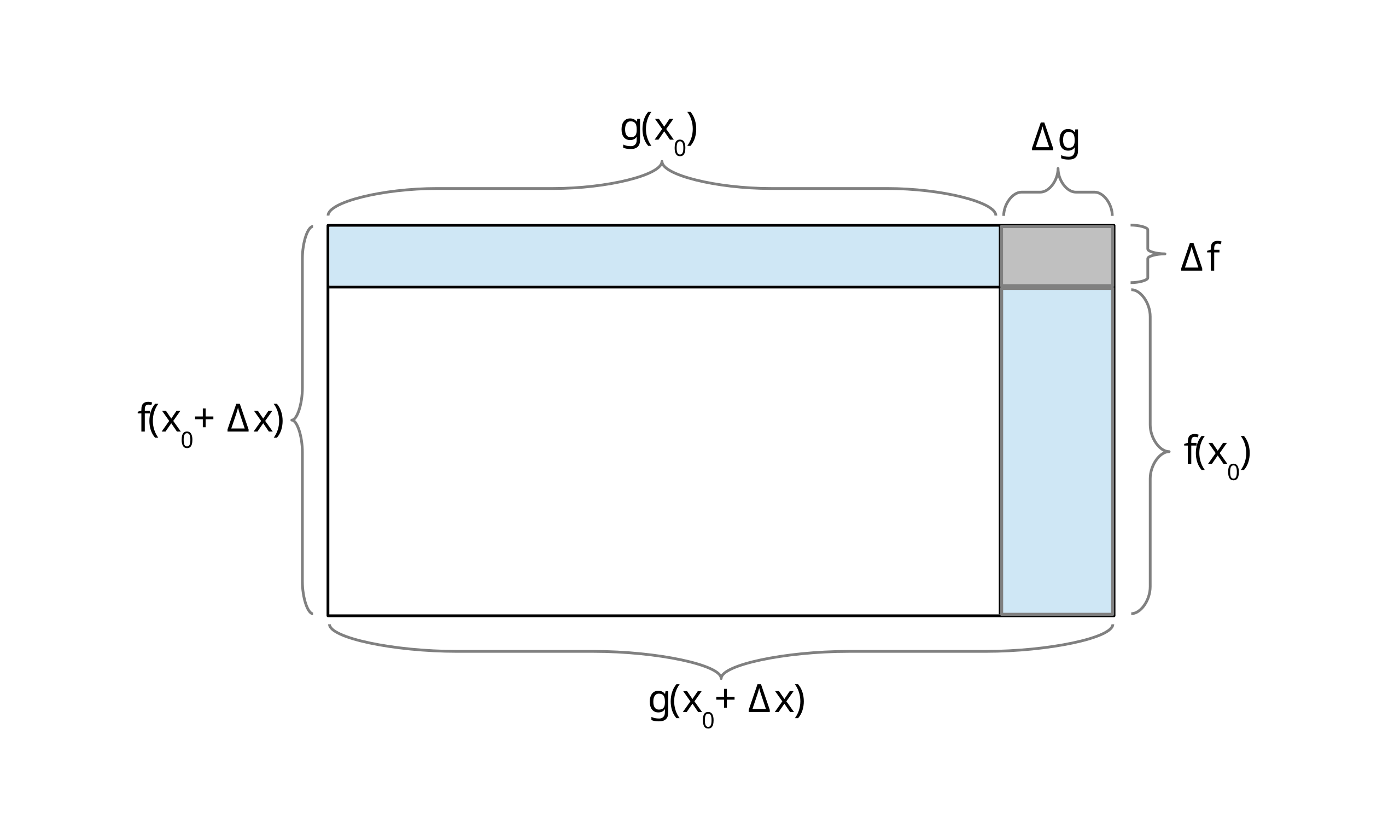
This diagram represents as the area of a rectangle, with the thin shaded strips showing the contributions from and . The small gray corner region represents the diminishing product of the two increments as they approach zero. The image includes and , which extend slightly beyond the syllabus wording but support an intuitive understanding of how the product rule arises. Source.
Because multiplication intertwines the behavior of both functions, differentiating the product cannot be handled by applying simpler derivative rules directly. The product rule provides a structured, reliable procedure for addressing this interaction and is essential when working with polynomial and power expressions that appear frequently in AP Calculus AB.
The Product Rule for Algebraic Functions
The product rule is the differentiation rule used when a function is defined as the product of two differentiable functions.

This formula displays the product rule , highlighting the structural pattern “first times derivative of second plus second times derivative of first.” The color-coding reinforces the relationship between each factor and its derivative. The image is limited to the required symbolic content for this subsubtopic. Source.
= first differentiable function
= second differentiable function
= derivative of
= derivative of
Because algebraic functions frequently combine multiple powers of , the product rule becomes an essential technique for decomposing expressions into manageable components.
Key Terminology and Structure
Before applying the rule, it is important to understand the components involved. A factor in algebra is one of the expressions being multiplied. When differentiating a product, each factor’s rate of change contributes to the slope of the entire function.
Factor: An expression multiplied by another expression to form a product.
This terminology is helpful for students as they learn to identify which parts of an expression play the roles of and when applying the product rule.
Recognizing this structure allows students to anticipate how the derivative will be constructed and to organize their work clearly and consistently.
Applying the Rule to Polynomial and Power Functions
Polynomial and power functions interact naturally with the product rule because they often appear in multiplicative combinations that cannot be simplified before differentiating. Expressions such as or are typical examples where the product structure should be identified immediately.
When applying the product rule to such algebraic expressions, students should adopt systematic habits that reduce errors and improve clarity. These habits are especially important under the time constraints and symbolic complexity of the AP Calculus AB exam.
Steps for Using the Product Rule Effectively
Students benefit from a consistent approach when differentiating products. A clear, repeatable process helps maintain accuracy as expressions grow in length or complexity.
Identify the two factors to be treated as and , ensuring each is clearly separated.
Differentiate each factor individually, applying the power rule or other basic derivative rules as appropriate.
Apply the structure of the product rule, forming the sum .
Simplify algebraically, combining like terms or factoring when helpful for clarity.
These steps emphasize both procedural fluency and algebraic organization, skills that AP Calculus AB students must master.
Importance of Algebraic Simplification
A derivative obtained using the product rule often contains multiple terms. Simplification is essential for interpreting results, comparing expressions, or preparing for subsequent operations such as setting derivatives equal to zero. Simplification may involve factoring, distributing, or rewriting expressions in equivalent forms.
Algebraic Simplification: The process of rewriting an expression in a clearer or more compact form without changing its value.
Students should remember that simplification is not merely cosmetic; it plays a functional role in preparing derivatives for further analysis in later topics such as curve sketching and optimization.
Common Situations Requiring the Product Rule
Algebraic functions frequently appear in product form in the following situations:
A monomial multiplied by a polynomial, as in
A binomial multiplied by another binomial, written in product form rather than expanded
A function written with factored expressions where expanding would be inefficient
Problems in applied contexts where quantities are defined as multiplicatively related
In each case, the product rule provides the appropriate framework for computing derivatives.
Avoiding Misconceptions
A common error occurs when students incorrectly assume that the derivative of a product is the product of derivatives. The product rule directly corrects this misconception by explicitly accounting for how both factors change. Another mistake arises when students attempt to apply the product rule even when expressions can be simplified before differentiating; however, when expressions truly remain in product form, the rule is essential.
Role of the Product Rule in Broader Calculus Understanding
Mastering the product rule prepares students for upcoming derivative rules involving trigonometric, exponential, and logarithmic functions. It also forms a foundation for later techniques such as implicit differentiation and related rates, both of which depend heavily on precise derivative computation.
FAQ
The product rule is required whenever the expression is genuinely a product of two functions of x, regardless of how simple one factor may appear.
A constant multiplier can be pulled out before differentiating, but any factor that varies with x contributes its own rate of change. Even a simple factor like x influences the derivative through its interaction with the other factor, so omitting the product rule leads to incorrect results.
A useful strategy is to look for multiplication signs that cannot be eliminated by straightforward algebraic simplification.
Common indicators include:
• Brackets placed directly next to another expression.
• A power term multiplied by a binomial or polynomial.
• Expressions left in factored form to avoid unnecessary expansion.
If simplification does not remove the product, the product rule will be required.
Expanding a product may eliminate the need for the product rule, but it is not always the best choice.
Expansion is helpful when:
• The expression expands cleanly into a small number of terms.
• Simplifying first reduces complexity.
However, expanding is inefficient when it produces many terms or increases the chance of algebraic mistakes. In those cases, applying the product rule directly is more reliable.
Typical errors include:
• Forgetting to differentiate both factors.
• Mixing up which derivative corresponds to which function.
• Dropping brackets when substituting f and f' or g and g'.
• Combining unlike terms or expanding incorrectly during simplification.
Carefully writing each step before simplifying greatly reduces these mistakes.
Products of functions often represent quantities where two changing variables interact, such as area with changing length and width or cost depending on both price and quantity.
The product rule captures how changes in each component jointly affect the total.
Understanding this interaction helps explain why the derivative of a product reflects contributions from both factors rather than a single combined rate of change.
Practice Questions
Question 1 (1–3 marks)
Differentiate the function h(x) = x^3(2x − 5).
Give your answer in simplified form.
Question 1 (1–3 marks)
• 1 mark: Correct application of the product rule: h'(x) = 3x^2(2x − 5) + x^3(2).
• 1 mark: Correct expansion of both terms (for example: 6x^3 − 15x^2 + 2x^3).
• 1 mark: Correct simplification: h'(x) = 8x^3 − 15x^2.
Total: 3 marks.
Question 2 (4–6 marks)
A function is defined by F(x) = (x^2 − 4)(3x^3 + 1).
(a) Use the product rule to find F'(x).
(b) Hence, determine the value of F'(2).
(c) Briefly explain why the product rule is required instead of differentiating the factors separately and multiplying the results.
Question 2 (4–6 marks)
(a)
• 1 mark: Correct structure using the product rule: (x^2 − 4)'(3x^3 + 1) + (x^2 − 4)(3x^3 + 1)'.
• 1 mark: Correct derivatives of each factor: (x^2 − 4)' = 2x and (3x^3 + 1)' = 9x^2.
• 1 mark: Substitution into the product rule: 2x(3x^3 + 1) + (x^2 − 4)(9x^2).
• 1 mark: Correct expansion or fully correct simplified form.
(b)
• 1 mark: Correct substitution of x = 2 into the derived expression.
• 1 mark: Correct numerical value for F'(2).
(c)
• 1 mark: Appropriate explanation that the derivative of a product is not equal to the product of derivatives, so the product rule is required.
Total: 6 marks.

