AP Syllabus focus:
‘Draw a diagram, label variables, and clearly identify which quantities and rates are given and which rate must be found before writing equations for a related rates problem.’
When approaching related rates problems, creating a clear diagram and identifying all quantities and rates is essential for organizing information, revealing relationships, and preparing equations for differentiation.
Drawing Diagrams in Related Rates Problems
A well-constructed diagram provides a visual representation of how quantities interact and change. It allows you to connect the context of the scenario to the mathematical relationships required for solving rate problems.
Purpose of a Diagram
A diagram helps convert a verbal description into a structured mathematical picture. This visual structure is especially important because related rates questions often involve multiple changing quantities that must be connected through an equation.
Shows geometrical or physical relationships.
Highlights which variables depend on time.
Helps identify where known values apply.
Clarifies the spatial arrangement or proportional relationships between quantities.
When sketching a diagram, aim for clarity rather than artistic precision.
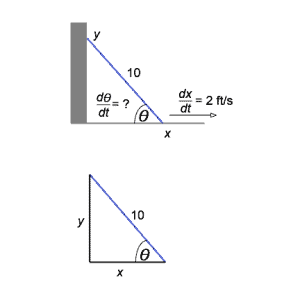
This figure shows a ladder leaning against a vertical wall, forming a right triangle with clearly labeled distance and angle measures. It demonstrates how a basic sketch helps translate a physical situation into variables for a related rates problem. The diagram reflects the kind of clear labeling essential for connecting geometry to changing quantities. Source.
The diagram should communicate how the components of the problem relate so you can assign variables consistently.
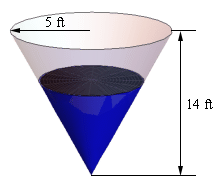
The illustration depicts an inverted conical tank with the water’s height and radius labeled separately from the tank’s constant dimensions. This emphasizes the distinction between fixed values and time-dependent variables in related rates setups. The diagram is a clear example of how labeled geometry prepares students for forming relationships between quantities. Source.
Labeling Quantities in a Diagram
Every diagram must include variable labels that connect directly to the wording of the problem. Labeling ensures that each changing measurement has a mathematical placeholder.
When labeling:
Assign meaningful variable names such as x for horizontal distance, h for height, or r for radius.
Indicate any fixed values (constants) separately from variables that change with time.
Mark angles or lengths explicitly if they are part of the geometric structure.
A clearly labeled diagram becomes a reference point for identifying how the variables relate through geometry, algebra, or trigonometry.
Identifying Given Quantities and Given Rates
After drawing and labeling the diagram, you must determine which quantities are given, which are changing, and what rate you are asked to find.
Understanding Rates in Context
A rate in a related rates problem is a derivative with respect to time. These represent how fast a quantity is changing as time progresses.
Rate of Change: A derivative expressing how one quantity varies with respect to another variable, typically time.
A standard related rates problem provides one or more known rates, such as a changing length, angle, or area. These rates must be recognized as derivatives.
How to Identify Given Rates
Given rates typically appear in the problem as phrases involving per unit time, such as “increasing at 3 cm/s” or “decreasing at 2 liters/min.” These translate into symbolic derivatives:
Length changing: dx/dt
Radius changing: dr/dt
Area changing: dA/dt
Look for language cues:
“Increasing” corresponds to a positive rate.
“Decreasing” corresponds to a negative rate.
“At that instant” indicates the moment for substituting numerical values.
Identifying the Unknown Rate
The unknown rate is the quantity the problem asks you to determine. It is always a derivative with respect to time and should connect directly to the labeled diagram.
To identify the target rate:
Look for statements such as “How fast is…,” “Find the rate at which…,” or “Determine the instantaneous rate of change of….”
Express this unknown symbolically, such as dy/dt, dθ/dt, or dV/dt, depending on the variable involved.
After identifying the variable whose rate is needed, ensure you understand how it relates to the other variables in the problem. This connection becomes essential when forming the equation to be differentiated.
Organizing All Quantities Before Writing an Equation
Before you create the equation that relates the variables, it is important to organize your known and unknown rates.
Checklist for Organizing Quantities
Variables: List all symbols representing changing quantities.
Known Values: Identify any numerical information provided, such as a specific length or angle at a particular instant.
Given Rates: Write down the derivatives you know.
Unknown Rate: Clearly state the derivative you must find.
Keeping quantities organized prevents errors when substituting values after differentiating.
Preparing for the Relationship Equation
A diagram, when paired with a list of known and unknown rates, guides the selection of the equation relating the variables. This equation may arise from geometry (perimeter, area, volume), algebraic relationships, or trigonometric identities.
General Rate Form: d(Quantity)/dt
d(Quantity)/dt = The rate at which that quantity changes with respect to time
This equation structure reflects the underlying principle that all related rates involve differentiating with respect to time, even when the original relationship uses geometric or algebraic forms.
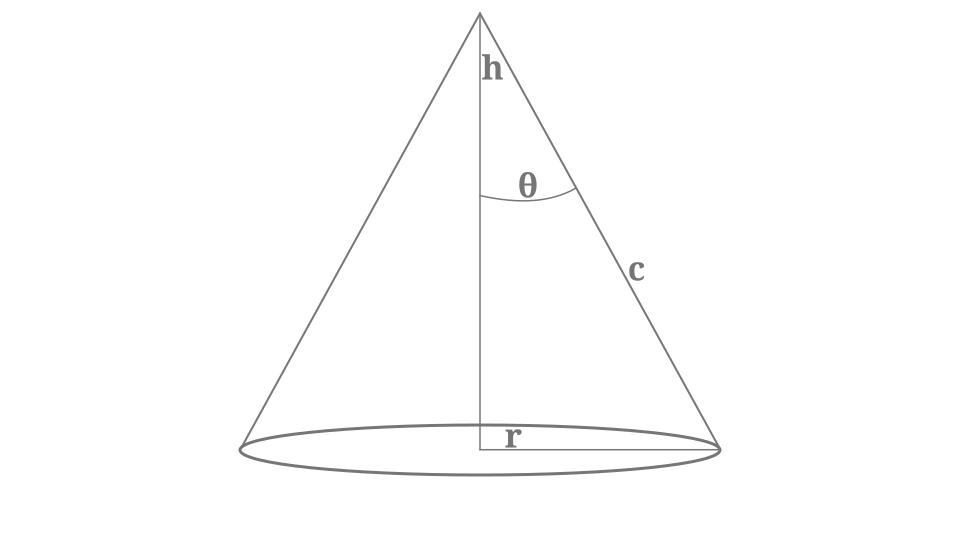
The diagram presents a cone with its radius, height, slant side, and apex angle labeled clearly. It serves as an example of precise variable labeling on geometric figures to support forming equations in related rates contexts. The inclusion of slant height and angle extends slightly beyond typical AP needs but remains consistent with clear diagramming practice. Source.
Because related rates problems can use various mathematical relationships, the diagram and variable identification steps ensure that the equation chosen correctly represents the context.
Final Organizational Notes for Related Rates Setup
Good organization before differentiating prevents mistakes and ensures clarity. When this groundwork is done carefully, the differentiation step becomes significantly more straightforward. A clear diagram, properly labeled variables, and correctly identified rates form the foundation of every successful related rates solution.
FAQ
A diagram should include only the elements needed to understand how the quantities in the problem relate. Unnecessary decoration or realistic detail is unhelpful.
Include:
• Key geometric shapes
• Labels for all changing variables
• Any fixed measurements relevant to the relationships
A minimal but accurate diagram reduces cognitive load and helps avoid incorrect assumptions about the situation.
Labelling a variable assigns a symbol to a changing quantity, such as height or distance. Identifying a rate refers to its derivative with respect to time.
A diagram shows variables visually, but rates are typically noted alongside the diagram, written in symbolic form. Both must be linked clearly to the same quantities, but they serve different organisational roles.
Check the wording carefully. Fixed dimensions are usually stated explicitly and do not depend on time. Changing quantities are implied through movement, flowing fluids, expansion, or shrinking.
Ask yourself:
• Can this measurement logically vary as the scenario evolves?
• Does the problem describe it as increasing or decreasing?
• Is it tied to another value that changes over time?
Many real-world rate problems involve geometric relationships where formulas for length, area, or volume already exist. Using established shapes simplifies finding an equation that connects variables.
Right triangles allow the use of trigonometric relations.
Cones and spheres have well-known volume formulas.
This consistency lets you convert the diagram into a mathematical relationship with minimal extra work.
Students often confuse a static measurement with a rate, or overlook that a quantity described as increasing or decreasing is a rate rather than a value.
Typical errors include:
• Treating a speed or flow rate as a length or volume
• Ignoring negative signs when something is decreasing
• Misidentifying which variable a rate corresponds to
Reading slowly and connecting each verbal rate to the labelled diagram helps prevent these issues.
Practice Questions
Question 1 (1–3 marks)
A spherical balloon is being inflated, and its radius increases at a constant rate. A diagram of the balloon is provided, showing the radius labelled r. At a certain instant, the radius is 5 cm and increasing at 0.4 cm per second.
State the given rate, identify the variable whose rate is required, and explain why drawing and labelling a diagram is helpful before forming any equations.
Question 1 (1–3 marks)
1 mark: Correctly identifies the given rate as dr/dt = 0.4 cm per second.
1 mark: Correctly identifies the required rate (such as the rate of change of volume with respect to time or another contextually reasonable rate specified by the problem).
1 mark: Provides a clear explanation that a labelled diagram helps visualise the changing quantities, ensuring the correct assignment of variables and avoiding errors before forming equations.
Question 2 (4–6 marks)
A trough has triangular cross-sections, each an isosceles triangle with a fixed base of 2 metres and a fixed height of 1 metre. Water is being poured into the trough, and the depth of the water at time t is h metres. A diagram is provided showing the cross-section with all dimensions labelled.
(a) Identify the variables that change with time and the quantities that remain constant.
(b) State the given rate and the rate that must be found.
(c) Explain how the diagram helps determine a relationship between the width of the water surface and the depth h before differentiating with respect to time.
Question 2 (4–6 marks)
1 mark: Correctly identifies the time-dependent variables, typically h and any related width variable that depends on h.
1 mark: Correctly identifies the constants, namely the fixed dimensions of the triangular cross-section.
1 mark: States the given rate clearly, such as dh/dt or a rate of volume increase/decrease, depending on the context.
1 mark: States the unknown rate that must be found, such as dV/dt or another rate logically implied by the problem.
1–2 marks: Provides a clear explanation that the diagram shows the similarity between the full triangular cross-section and the water-filled triangle, allowing one to relate width to depth by geometric proportions before writing an equation.

