AP Syllabus focus:
‘Understand that related rates problems involve two or more related quantities whose rates of change are connected through an equation, often with time as the common independent variable.’
Related rates situations describe how interconnected quantities change at the same instant. By expressing their relationship with an equation and differentiating, we uncover how one rate depends on another.
Understanding the Structure of Related Rates Situations
A related rates situation always centers on multiple quantities changing simultaneously, typically within a physical, geometric, or contextual setting.
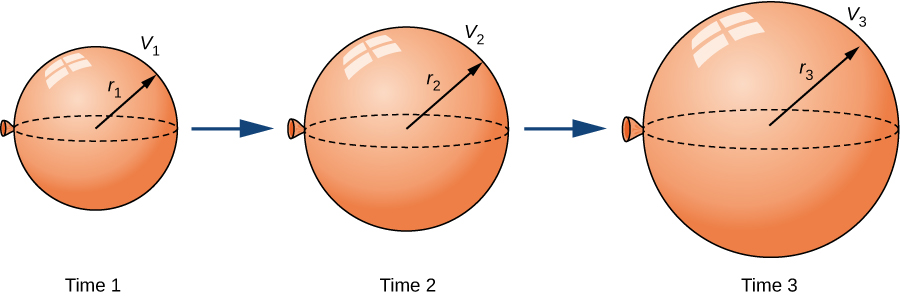
A spherical balloon is shown at three successive times, with both the radius and the volume increasing as time passes. This visual emphasizes that a single physical situation can involve several quantities changing together and related by an equation, such as a volume formula. The diagram includes labels for different radii and volumes but no additional calculations beyond the conceptual level required here. Source.
Time as the Common Independent Variable
Most related rates problems treat time as the shared independent variable because many real-world phenomena evolve dynamically. When one quantity changes over time, any other quantity determined by it must also change as time progresses. This makes the natural reference point for all derivatives in these problems.
Changing Quantities and Their Relationships
To analyze a related rates context, students must distinguish clearly between:
Variables representing quantities that change, such as length, area, volume, or angle.
Rates of change, often expressed in derivative notation like or .
Equations that tie the variables together, such as geometric formulas, motion relationships, or physical laws.
Because these quantities evolve at the same instant, the derivative of one variable often influences the derivative of another, revealing the interconnected nature of the situation.
When the term related quantities is used, it refers to quantities whose values depend on one another through an explicit or implicit mathematical relationship.
Related Rates: A technique in calculus for determining how the rate of change of one quantity is connected to the rate of change of another when both depend on the same independent variable.
Recognizing the underlying relationship is essential for expressing how a change in one variable propagates through the system.
The Role of Equations in Related Rates Situations
A distinguishing feature of related rates is that the connection between variables must be written before differentiation occurs. This equation represents the structure of the situation and ensures that each variable's rate is accounted for properly.
Why Differentiation Links the Rates
Differentiating the equation with respect to time applies the chain rule, automatically incorporating rates of change for every variable involved. Even when only one variable appears to change explicitly, differentiation reveals the often-hidden dependence on time.
= A function expressing the relationship between variables (unit varies)
= Dependent variables that change over time (units determined by context)
= Rates of change of the variables with respect to time (units per second, or as appropriate)
This formulation illustrates how each variable’s derivative emerges naturally from implicit differentiation.
The presence of multiple interacting derivatives underscores the central requirement of related rates: all derivatives must be taken with respect to the same independent variable, typically time.
Identifying a Related Rates Situation
Students should look for certain features indicating that a scenario belongs to this category of problems:
Key Indicators
Two or more quantities are changing at an instant.
The quantities are linked by a mathematical or geometric relationship.
A rate is given, and another rate is requested.
Time is explicitly or implicitly involved as the independent variable.
Common Contextual Signals
Related rates situations often appear in contexts such as:
Geometric growth or shrinkage, where lengths, areas, and volumes depend on one another.
Motion, where distances or angles change simultaneously.
Physical systems, including flow, expansion, or rotation.
While contexts vary widely, the structural pattern does not.
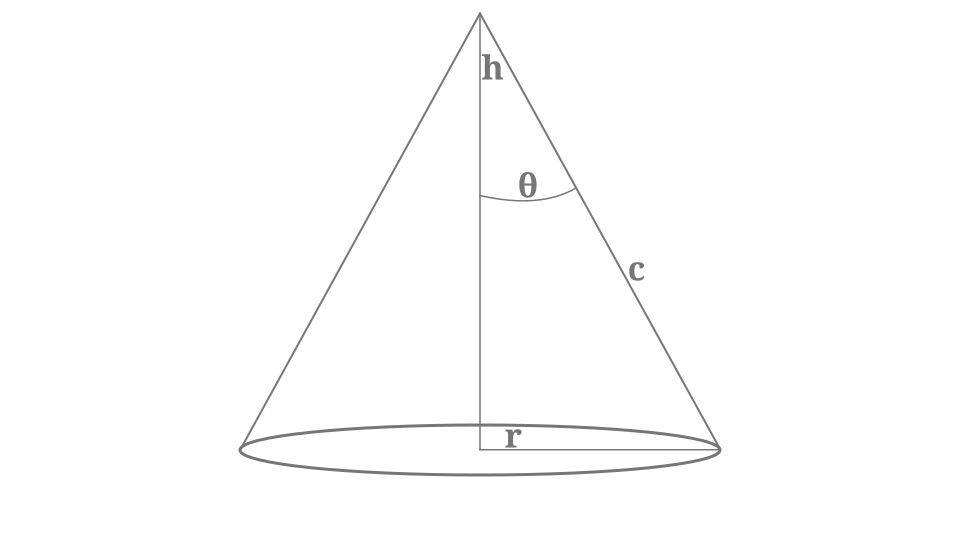
A right circular cone is shown with its radius r, height h, slant height c, and angle θ clearly labeled. This diagram highlights how several geometric measurements can be linked in a single object, providing the structural relationship that later allows their rates of change to be connected through differentiation. The inclusion of the slant height c and angle θ goes beyond the minimum needed for this subsubtopic but remains consistent with the idea of multiple related quantities in a single context. Source.
The analysis requires identifying variables, establishing their relationship, and understanding the interplay of derivatives.
When students encounter phrases like “how fast,” “rate of change,” or “changing at the instant when,” they are typically being asked to interpret or compute a related rate.
Instantaneous Rate of Change: The value of a derivative describing how quickly a quantity changes at a single moment in time.
Recognizing such language helps students frame the problem correctly before proceeding to later steps, such as drawing diagrams or applying differentiation rules.
Conceptual Goals for Students
By mastering this subsubtopic, students should be able to:
Interpret related rates situations clearly and identify the changing quantities.
Recognize the necessity of expressing the relationship among variables before differentiation.
Understand why time serves as the most common independent variable.
Describe how differentiating a relationship reveals how one rate depends on another.
These conceptual foundations prepare students for the procedural steps in subsequent subtopics involving diagram construction, equation setup, and systematic differentiation.
FAQ
You should treat time as the independent variable when the quantities in the scenario evolve as a process unfolds. If something is growing, shrinking, moving, filling, draining, or changing shape over a duration, time is implicitly driving the change.
Time is also appropriate when:
A description includes words such as instantly, per second, or at that moment.
The context involves a physical process, even if time is not explicitly mentioned.
Substituting too early removes the variables’ dependence on one another, which eliminates the ability to connect their rates of change. Related rates rely on the idea that the variables are still changing at the instant in question.
You substitute numerical values only after differentiating, when you are ready to evaluate the rate at a specific moment.
Yes. Some situations involve several interconnected variables, all changing with time. Each contributes a derivative term when differentiating the relationship.
For example:
A geometric shape with multiple dimensions changing simultaneously
A physical system where distance, angle, and speed all vary
The key requirement is that all variables must be related through an equation before differentiation.
A suitable relationship must express how the variables depend on one another without already involving rates. It can come from geometry, physics, or the way quantities are defined.
You should check that:
The equation holds for all valid values of the variables
The variables represent measurable quantities
The relationship can be differentiated implicitly with respect to time
A negative rate indicates that the quantity is decreasing at that instant. This contrasts with a positive rate, which indicates growth.
In a related rates context:
One variable may increase while another decreases
Signs help interpret direction, physical behaviour, or whether a system is contracting or expanding
Negative rates often appear in contexts such as draining, shrinking, or approaching a fixed point.
Practice Questions
Question 1 (1–3 marks)
A quantity y depends on a quantity x, and both vary with time t. At the instant when x = 5, the rate dx/dt is 3 units per second. Explain what it means to say that dy/dt represents the instantaneous rate of change of y at this instant.
Question 1 (1–3 marks)
1 mark: States that dy/dt describes how fast y is changing at a particular moment in time.
1 mark: Recognises that dy/dt is the instantaneous rate, not an average over an interval.
1 mark: Makes clear that the rate is measured per unit time and depends on the behaviour of y as x (and time) change.
Question 2 (4–6 marks)
A circular patch of water on the ground is expanding as rain falls, and its radius r and area A both change with time t.
The relationship between A and r is A = πr².
At a certain instant, the radius is increasing at a rate of 0.4 metres per second, and the radius is 2.5 metres.
(a) Explain why this is a related rates situation.
(b) Using the relationship between A and r, find dA/dt at this instant.
(c) Interpret the meaning of the value of dA/dt in the context of the situation.
Question 2 (4–6 marks)
(a)
1 mark: Identifies that both A and r are changing with time.
1 mark: States that the variables are linked by the geometric equation A = πr², so their rates must also be connected.
(b)
1 mark: Differentiates A = πr² with respect to time to obtain dA/dt = 2πr dr/dt.
1 mark: Substitutes r = 2.5 and dr/dt = 0.4 correctly.
1 mark: Computes the numerical result dA/dt = 2π(2.5)(0.4) = 2π.
(c)
1 mark: Interprets the value as the area increasing at 2π square metres per second at that instant.
1 mark: Clearly connects the rate to the physical expansion of the water patch at that moment.

