AP Syllabus focus:
‘Recognize when the limit of a ratio of two functions produces the forms 0/0 or ∞/∞, and understand that such expressions are called indeterminate because the limit is not immediately known.’
Indeterminate forms arise when evaluating limits leads to expressions that do not directly reveal predictable behavior, requiring deeper analysis to determine how two related quantities behave near a point.
Understanding Indeterminate Forms in Limits
Indeterminate forms appear when the structure of a limit expression does not uniquely determine the limit’s value. In AP Calculus AB, this idea is essential for understanding why some limits cannot be found through direct substitution and why special techniques, such as L’Hospital’s Rule, become necessary later. When two competing behaviors interact—such as a numerator and denominator both approaching zero or both increasing without bound—the limit may take many possible values depending on how each component behaves. These situations require students to look beyond surface-level expressions and analyze the underlying functions more carefully.
What Makes a Form Indeterminate
An indeterminate form occurs when evaluating a limit yields a symbolic expression that does not provide enough information to determine the actual limit. At this stage, “indeterminate” does not mean “undefined.” Instead, it signals that more work is required to determine the true limit. This distinction is important: an indeterminate form represents a structural ambiguity, not a failure of mathematics.
Indeterminate Form: A limit expression whose initial evaluation does not uniquely determine the limit’s value because multiple limit outcomes are possible depending on functional behavior.
Recognizing these forms early allows students to avoid misinterpretations such as assuming that equals , or that equals . Neither conclusion is valid, and making such assumptions can lead to incorrect results or misapplied techniques.
The Two Indeterminate Forms in AP Calculus AB
The AP Calculus AB curriculum focuses specifically on two primary indeterminate forms that arise from ratio expressions:
The 0/0 Indeterminate Form
When substitution in a limit causes both the numerator and denominator to approach zero, the expression is said to be of the 0/0 form. This form signals a delicate balance between two quantities shrinking at possibly different rates. Depending on the functions involved, such a limit could evaluate to any real number, zero, infinity, or fail to exist altogether. Students must understand that the behavior of the numerator relative to the denominator determines the result, not the symbolic appearance of zeros alone.
= The numerator approaches zero
= The denominator approaches zero
Different functions can all produce the symbol 0/0 at a point, yet their limits can be , , some other finite number, , or may fail to exist altogether.
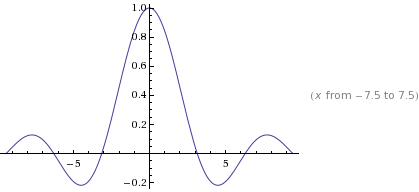
Graph of near , illustrating a classic indeterminate form. The curve approaches even though substitution produces . This shows that the symbolic form alone does not determine the limit. Source.
A 0/0 result encourages further analysis to compare how rapidly each part approaches zero. Without that comparison, the limit remains unknown.
The ∞/∞ Indeterminate Form
The second major form involves a ratio in which both the numerator and the denominator grow without bound. An expression of the form does not imply that the limit equals simply because both quantities are large. Instead, it highlights competing unbounded behaviors that must be resolved. One function may increase faster, slower, or at a comparable rate to the other, producing a wide range of possible limit values.
= The numerator increases without bound
= The denominator increases without bound
That is why expressions of the form 0/0 or ∞/∞ in a limit are called indeterminate forms: they signal that further analysis is required before the limit can be known.
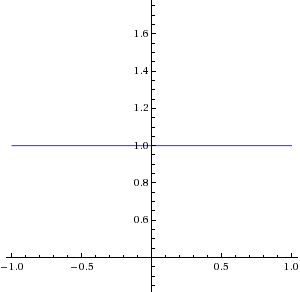
Graphs showing multiple functions that all produce the symbolic form at a point but yield different limits. Some approach finite numbers, others diverge, demonstrating why and are indeterminate. The image includes extra example curves beyond the syllabus, but all reinforce the concept of variability behind an indeterminate form. Source.
Why Indeterminate Forms Require Additional Techniques
Recognizing indeterminate forms prevents premature evaluation and alerts students to use more advanced tools. The syllabus emphasizes that these forms do not reveal the limit’s value immediately. Instead, they provide a starting point for deeper investigation. Later techniques, such as algebraic manipulation, strategic rewriting, or eventually L’Hospital’s Rule, help uncover the true limit. Understanding the nature of indeterminate forms is therefore foundational to both conceptual reasoning and problem-solving in AP Calculus AB.
How to Identify Indeterminate Forms
Students should develop habits of detection by examining the behavior of the numerator and denominator separately. Useful strategies include:
Substituting the limit value only to determine behavior, not the final result.
Noting whether each part approaches zero, a finite number, or infinity.
Watching for symbolic cues such as or that indicate the limit is not yet resolved.
Avoiding assumptions that these symbolic expressions behave like numerical fractions.
Identifying an indeterminate form is a skill that improves with practice and reinforces a deeper understanding of function behavior.
The Importance of Context in Indeterminate Expressions
Indeterminate forms are contextual results. The same symbolic form may lead to different limits depending on the functions. For example, two functions approaching zero might do so at drastically different rates, producing dramatically different outcomes. This reinforces the syllabus statement that such expressions “are called indeterminate because the limit is not immediately known.” Students should appreciate that the symbol alone never determines the answer; only the underlying functional relationship does.
By mastering the recognition of indeterminate forms, students build a strong conceptual foundation for the analysis of complex limit expressions encountered throughout AP Calculus AB.
FAQ
AP Calculus AB focuses on foundational reasoning around limits, so only the two indeterminate forms directly connected to L’Hospital’s Rule are assessed.
Other forms, such as 0 multiplied by infinity or infinity minus infinity, can often be rewritten into one of the two required ratio forms through algebraic manipulation.
This ensures that students concentrate on understanding why a ratio may fail to reveal a limit, rather than memorising a larger catalogue of possible forms.
Yes. Many limit expressions initially appear as 0/0 or infinity/infinity even though algebraic simplification removes the issue.
A classic example is when a common factor in the numerator and denominator cancels, eliminating the source of the indeterminate form.
Indeterminacy refers only to what happens before simplification; once rewritten, the limit can often be found directly.
Not unpredictably, but their competing behaviours make the limit unclear without further work.
Two functions may decrease or grow at consistent rates, but unless their relationship is examined, it is impossible to know whether they balance out, dominate each other, or oscillate.
Indeterminate forms simply indicate that the outcome is not obvious from structural inspection alone.
Yes. A limit can be determinate, such as a non-zero number over zero or a finite number over infinity, yet still require algebraic insight to compute precisely.
Determinate forms indicate that the general type of limit behaviour is known, but they do not guarantee that the numerical value is trivial to determine.
Indeterminate forms, by contrast, prevent even general predictions.
Because many real functions behave similarly near zeros or extremes, producing expressions where both numerator and denominator shrink or grow at comparable rates.
Such situations naturally create ratios like 0/0 or infinity/infinity, especially when modelling rates, densities, or quantities that approach limiting behaviours.
Indeterminate forms signal that these subtle interactions require closer examination before meaningful conclusions can be drawn.
Practice Questions
Question 1 (1–3 marks)
When evaluating the limit of a ratio of two functions as x approaches 4, direct substitution gives 0/0.
(a) State why 0/0 is called an indeterminate form.
(b) Explain what this result tells you about the limit.
Question 1
(a) 1 mark: States that 0/0 is indeterminate because it does not determine a unique limit or can lead to many different possible limit values.
(b) 1–2 marks:
• 1 mark for stating that the limit cannot be concluded from 0/0 alone.
• 1 mark for explaining that further analysis (such as algebraic simplification or another method) is required to find the actual limit.
Total: 2–3 marks.
Question 2 (4–6 marks)
A student is analysing the limit of a function f(x) and determines that both the numerator and denominator of f(x) grow without bound as x approaches a particular value.
(a) Identify the indeterminate form present.
(b) Explain clearly why this form does not determine the value of the limit.
(c) Describe what additional reasoning or analysis would be required before the limit can be evaluated.
Question 2
(a) 1 mark: Correctly identifies the indeterminate form as infinity over infinity.
(b) 1–2 marks:
• 1 mark for stating that the form does not uniquely determine the limit.
• 1 mark for explaining that different functions approaching infinity can do so at different rates, leading to different possible limit values.
(c) 2–3 marks:
• 1 mark for stating that further analysis is required (such as comparing growth rates).
• 1 mark for naming an appropriate method (e.g., algebraic manipulation or L’Hospital’s Rule, even though not applied here).
• 1 mark for explaining that the behaviour of the numerator and denominator near the point must be examined before the limit can be determined.
Total: 4–6 marks.

