AP Syllabus focus:
‘Verify that the hypotheses of L’Hospital’s Rule are satisfied by checking that the original limit gives an indeterminate form and that the derivative of numerator and denominator exist near the point.’
Understanding when L’Hospital’s Rule may be applied is essential, because the rule only works under specific mathematical conditions that ensure the resulting limit is valid and meaningful.
Conditions for Applying L’Hospital’s Rule
L’Hospital’s Rule provides a powerful tool for evaluating limits that initially appear undefined. However, its use is restricted to situations where the structure of the limit meets certain mathematical requirements. These requirements ensure that replacing a difficult limit with the limit of a ratio of derivatives does not change the value of the limit itself. Students must be able to identify when these conditions are satisfied and when they are not, so that the rule is applied correctly and appropriately in AP Calculus AB contexts.
Indeterminate Forms as the Starting Point
A crucial requirement for applying L’Hospital’s Rule is that the original limit must produce an indeterminate form. This concept is fundamental because indeterminate expressions cannot be evaluated directly.
Indeterminate Form: An expression such as 0/0 or ∞/∞ whose limit cannot be determined from the form alone and requires additional analysis.
Before using the rule, students must analyze the behavior of the numerator and denominator separately as the variable approaches the limit value. Only if both parts tend toward zero or both tend toward positive or negative infinity does the limit qualify as an indeterminate form requiring further techniques. Situations where the limit forms a determinate expression, such as nonzero divided by zero or zero divided by a nonzero constant, do not qualify for the use of this rule.
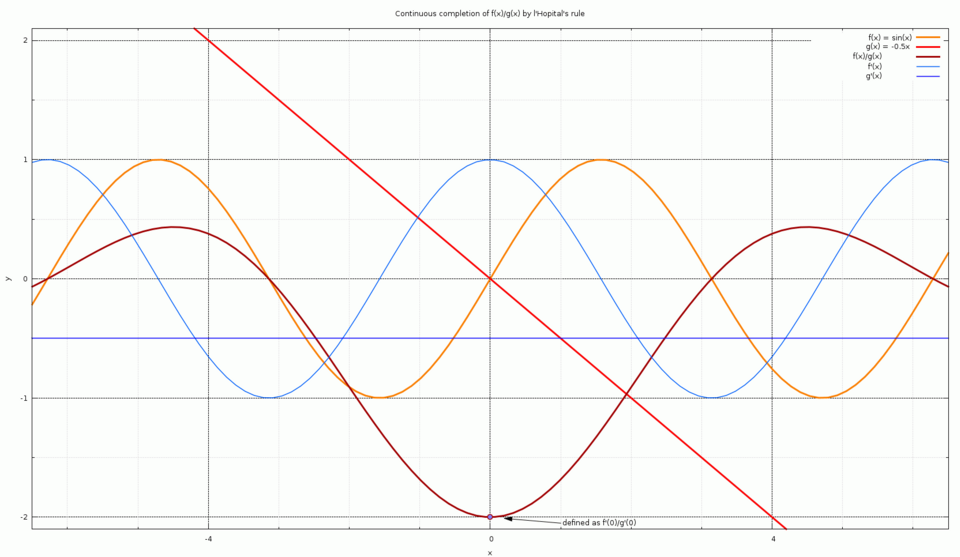
Graph of the functions f(x)=sinxf(x)=\sin xf(x)=sinx, g(x)=−0.5xg(x)=-0.5xg(x)=−0.5x, their quotient, and their derivatives. The point at x=0x=0x=0 shows how f′(0)/g′(0)f'(0)/g'(0)f′(0)/g′(0) provides a continuous extension. This image includes more detail than required for AP Calculus AB but effectively illustrates how derivative existence and a nonzero denominator derivative allow L’Hospital’s Rule to determine a meaningful limit. Source.
Ensuring Differentiability and Existence of Derivatives
Even if a limit is of indeterminate form, this alone is not sufficient grounds for applying L’Hospital’s Rule. The functions in the numerator and denominator must also be differentiable on an open interval containing the point of interest, except possibly at the point where the limit is taken. This requirement ensures that the derivatives used in the rule are properly defined.
Differentiable Function: A function that has a derivative at every point in an open interval, meaning its instantaneous rate of change exists throughout that interval.
The existence of the derivatives of both the numerator and denominator near the point is necessary because L’Hospital’s Rule replaces the original limit with a new one involving the derivatives. If either derivative does not exist or is discontinuous in a crucial region, the rule becomes invalid. Additionally, the denominator’s derivative must not be zero throughout the relevant interval, because dividing by a zero derivative would lead to an undefined or misleading expression.
Structure of the Limit and Its Required Form
L’Hospital’s Rule applies only to limits where the structure matches the ratio of two functions approaching a point or tending toward infinity. The rule requires that the limit initially be presented in fractional form so that both numerator and denominator can be differentiated meaningfully.
= Original limit structure
= Numerator function
= Denominator function
After confirming this structure and verifying that both functions satisfy the differentiability requirements, the rule states that the original limit may be replaced with the limit of the derivatives, provided all other conditions hold. Although the rule is often applied iteratively if another indeterminate form appears, each application still demands that every condition be rechecked before proceeding.
A correctly structured limit is essential because the rule cannot be applied to expressions that are not written as ratios. Students may need to rewrite or algebraically manipulate limits to achieve the proper form before analyzing whether the rule is appropriate.
Checking the Limit of the Derivative Ratio
A final requirement is that the limit of the ratio of derivatives must exist or approach positive or negative infinity. L’Hospital’s Rule does not guarantee that differentiating will resolve the indeterminate form, but it guarantees that if the derivative ratio has a limit, then that value is the limit of the original expression.
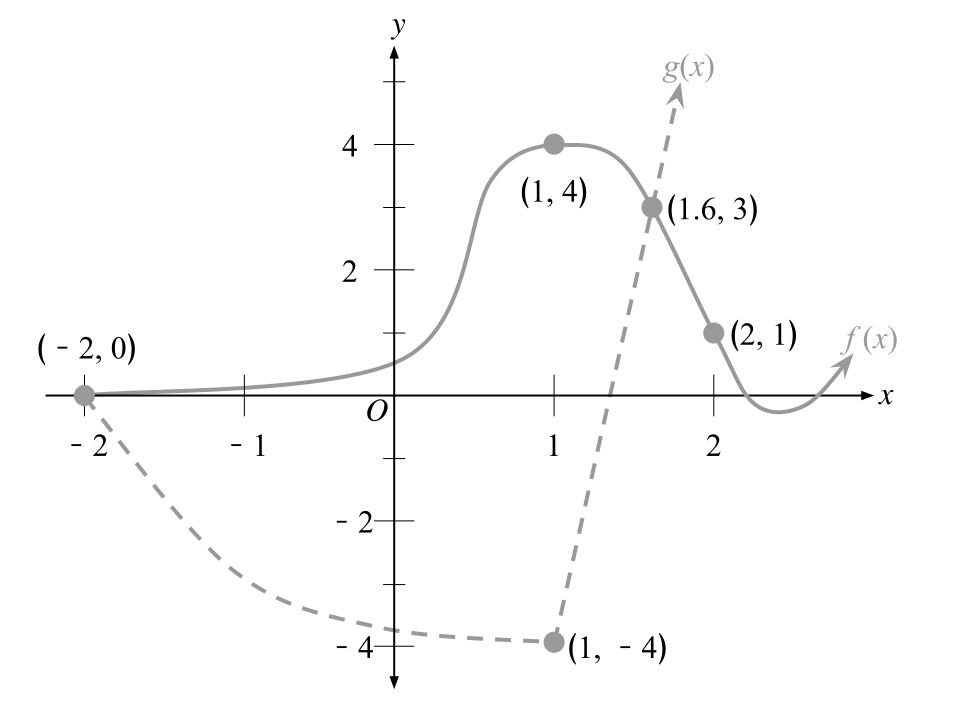
Graphing exercise illustrating how derivative information near a point determines the behavior of a quotient in L’Hospital’s Rule. Tangent slopes and function values guide students to interpret the derivative ratio f′(x)/g′(x)f'(x)/g'(x)f′(x)/g′(x). The image contains more graphical detail than required but reinforces the relationship between local slopes and the resulting limit. Source.
Students must examine whether applying the rule simplifies or clarifies the limit and must confirm that the resulting limit exists. If the derivative ratio does not exist or does not approach a finite value or infinity, the original limit remains unresolved, and different analytical methods must be used.
Summary of Required Conditions
To apply L’Hospital’s Rule correctly in AP Calculus AB, students must verify:
The limit produces an indeterminate form of 0/0 or ∞/∞.
Both numerator and denominator are differentiable on an interval around the point.
The derivatives exist and the denominator’s derivative is not zero near the point.
The limit can be expressed as a ratio of functions approaching a value or infinity.
The limit of the derivative ratio exists or approaches infinity.
These conditions ensure appropriate and accurate use of L’Hospital’s Rule in analyzing indeterminate limits.
FAQ
L’Hospital’s Rule relies on comparing how quickly two functions approach zero or infinity by examining the ratio of their derivatives. This comparison only makes sense when the original expression is structured as a quotient.
Other indeterminate forms, such as 0 multiplied by infinity or infinity minus infinity, must first be rewritten algebraically into a quotient before any of the rule’s conditions can be checked.
Check whether either function has a sharp turn, cusp, discontinuity, or vertical tangent close to the limit point.
Useful checks include:
• Confirming each function is defined on an open interval around the point.
• Verifying no algebraic form causes undefined behaviour (such as division by zero or log of a non-positive value).
• Using basic derivative rules to ensure both functions have derivatives that remain finite near the point.
Continuity at the limit point itself is not strictly required, but continuity on an open interval around that point is implied by differentiability.
A function may be undefined at the limit point and still satisfy the rule’s conditions, provided:
• It is differentiable on an open interval around the point (excluding the point itself).
• The limit of the derivatives exists and offers meaningful information about the original limit.
Successive indeterminate outcomes simply mean the limit cannot yet be resolved through a single differentiation.
You may:
• Continue applying L’Hospital’s Rule, provided each application still satisfies all conditions.
• Consider algebraic simplification or series expansion if repeated differentiation does not simplify the expression.
• Check for hidden structural issues, such as a derivative that oscillates or fails to approach a finite limit.
Yes. L’Hospital’s Rule guarantees a correct limit only when the derivative ratio has a limit.
Failure may occur when:
• The limit of the derivatives does not exist.
• The derivative ratio oscillates or diverges.
• The derivatives become undefined at points arbitrarily close to the limit.
In such cases, the rule does not provide information, and alternative limit techniques must be used.
Practice Questions
Question 1 (1–3 marks)
The limit below is to be evaluated using L’Hospital’s Rule.
lim as x approaches 0 of (e^x − 1) / (2x)
(a) State the indeterminate form that justifies the use of L’Hospital’s Rule.
(b) Verify that the conditions for applying L’Hospital’s Rule are satisfied.
Question 1 (Total 3 marks)
(a)
• 1 mark: Correctly stating that the limit is of indeterminate form 0/0.
(b)
• 1 mark: Stating that both numerator and denominator are differentiable near x = 0.
• 1 mark: Stating that the derivatives of numerator and denominator exist and the derivative of the denominator is non-zero at x = 0.
Question 2 (4–6 marks)
Consider the limit
lim as x approaches 3 of (ln(x) − ln(3)) / (x − 3).
(a) Explain why this limit has the correct structure for L’Hospital’s Rule.
(b) Show that the original limit produces an indeterminate form.
(c) Verify that the numerator and denominator satisfy the differentiability requirements for applying L’Hospital’s Rule.
(d) State whether L’Hospital’s Rule may be applied, giving a clear justification.
Question 2 (Total 6 marks)
(a)
• 1 mark: Identifying that the limit is written as a ratio of two functions approaching a point.
• 1 mark: Noting that both functions are real-valued functions of x.
(b)
• 1 mark: Correctly showing that ln(x) − ln(3) approaches 0 and x − 3 approaches 0, giving an indeterminate form 0/0.
(c)
• 1 mark: Stating that ln(x) is differentiable for x > 0, so it is differentiable at all values near x = 3.
• 1 mark: Stating that x − 3 is differentiable for all real x and its derivative is non-zero.
(d)
• 1 mark: Concluding that all conditions for L’Hospital’s Rule are satisfied and therefore the rule may be applied.

